Законы Ома и Кирхгофа в операторной форме. Пояснить принципы составления операторных схем замещения.

Пусть в цепи произошла коммутация и на её участке аb напряжение будет определяться интегро-дифференциальным уравнением

Рис. 2.2.

.

Отобразим это уравнение в операторную область, совершая над ним преобразование Лапласа

.

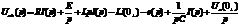Тот же результат можно получить если не отображать уравнение, а составить операторную схему замещения участка цепи ab.

Рис. 2.3.

Ток в операторной схеме замещения будет найден по закону Ома для участка, содержащего эдс.

.

Закон Ома в операторной форме

,                                (2.10)

где Z(p)- операторное сопротивление участка цепи;

-содержит изображения источников и источники, возникающие в следствие ненулевых начальных условий.

Выделим в цепи контур, составим его операторную схему замещения и для изображений токов и напряжений запишем уравнения по первому и по второму закону Кирхгофа.

Рис. 2.4.

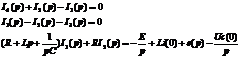
Законы Кирхгофа в общем виде

                                (2.11)

Вывод: если показать, что в операторной схеме замещения выполняются законы Кирхгофа, то следовательно её расчет может быть выполнен любым методом анализа линейных цепей (МКТ, МУП, МЭГ, метод наложения).

 

ОРИГИНАЛ			ИЗОБРАЖЕНИЕ

36.продолжение

Строим график:

 

Особенностью расчёта цепей данного класса является то, что, на его точность окажет сильное влияние идеализация ключевого и индуктивного элементов. Если допустить мгновенность размыкания, то на индуктивности возникнет бесконечно большое напряжение, но на практике такое невозможно. При резком изменении тока индуктивности может загореться дуга в размыкателе или возникнуть высокочастотный колебательный контур, образованный индуктивностью и распределённой межвитковой ёмкостью катушки. Часть энергии при такой коммутации неизбежно превратится в теплоту электрической дуги или будет излучаться в виде электромагнитных волн. Это означает, что электрическую цепь нельзя практически рассматривать как абсолютно замкнутую систему и нельзя ожидать точного выполнения обобщенного закона коммутации. Чем ближе свойства элементов цепи к своим идеализациям, тем точнее обобщенный закон коммутации описывает процесс в цепи.

Пути восстановления оригинала функции по известному ее операторному изображению.

Под p условимся принимать комплексное число p = d + jw (можно рассматривать как комплексную частоту). Функцию времени (ток, напряжение) обозначают f(t) и называют оригиналом. Ей соответствует функция F(p) – изображение. Соответствие F(p) = f(t) устанавливается с помощью преобразований:

- прямое преобразование Лапласа:

                                                                                                                                                                                                           (1)

- обратное преобразование Римана-Мелина:

                                                                                                                                                                                                     (2)

       Изображение напряжения на конденсаторе.

       Напряжение на конденсаторе uc часто записывают в виде:

,

где не указаны пределы интегрирования по времени. Более полной является следующая запись:

                               ,

где учтено, что к моменту времени t напряжение на конденсаторе определяется не только током, протекающим через C в интервале времени от 0 до t, но и тем напряжением uc(0), которое было на нем при t=0.

Поэтому:               .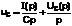

Простейшие операторные соотношения содержатся в справочном материале многих учебных пособий в виде готовых таблиц.

Отметим основные свойства преобразования Лапласа:

1) Соответствие между оригиналом и изображением взаимно однозначно: каждой функции f(t) соответствует F(p) и наоборот.

2) При умножении оригинала f(t) на постоянную величину a, умножается и изображение:

                                                      af(t) . = × aF(p) .

3) Изображение суммы функций равно сумме изображений этих функций.

Эта теорема позволяет по известному изображению функции в виде рациональной дроби:

найти соответствующий ей оригинал, где

B(p) = bmpm + bm-1pm-1 + … + b1p + b0 = bm (p–p1)(p–p2)…(p–pm) .

p1, p2, … , pm – корни уравнения B(p)=0.

Теорема разложения аналитически представляется формулой:

                                                       .

Доказательство:

 .

Из курса математики известно, что если n<m, ak и bk – вещественные числа, а корни p1, p2, … , pm уравнения B(p)=0 различные, то дробь  может быть представлена в виде суммы простых дробей:

 .

Для определения коэффициента A1 умножим обе части уравнения на (p–p1):

 .

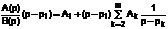Рассмотрим это выражение при p®p1. Правая часть дает A1, левая представляет собой неопределенность, так как множитель (p–p1) дает ноль, и знаменатель B(p) при p=p1 тоже обращается в ноль.

Раскроем неопределенность по правилу Лопиталя. С этой целью производную от числителя разделим на производную от знаменателя, и найдем предел дроби.

, где                                                                

B’(p) – производная от B(p) по p,

B’(p1) – значение B’(p) при p=p1,

A(p1) – значение A(p) при p=p1.

Следовательно, при p®p1 получаем уравнение:

 . Аналогично:  .

Таким образом,  .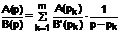

Пусть изображение какой-либо функции времени, например тока, представлено в виде дроби:

.

Перейдем от изображения к оригиналу. Оригиналом левой части является i(t). Оригинал правой части равен сумме оригиналов ее слагаемых. Так как множители 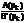 – есть постоянные числа, а функциями p являются множители , которым соот-вуют функции времени вида . Поэтому: .

Последовательность вычислений по формуле такова:

1) Приравниваем B(p) к нулю и определяем корни p1, p2, … ,pn.

2) Вычисляем производную B’(p) и подставляем в нее корни p1, p2, … ,pn (поочередно).

3) Подставляем в числитель корни p1, p2, … ,pn. Определяем его значения – A(pk).

4) Вычисляя отдельные слагаемые и суммируя их, определяем оригинал f(t).

Замечания к формуле разложения:

1) Формула разложения применима при любых начальных условиях и при любых практически встречающихся формах напряжения источника эдс или тока, воздействующего на схему.

2) Если уравнение B(p)=0 имеет комплексно-сопряженные корни, то слагаемые в формуле разложения оказываются также комплексно-сопряженными и в сумме дают действительное слагаемое.

 

 

31. Алгоритм расчета переходного процесса классическим методом в цепи первого порядка на примере подключения R-L-цепи к источнику синусоидального напряжения.

y-фаза коммутации

Рис. 1.6.

1. Записываем решение как сумму свободной и установившейся составляющих

.

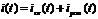2. Установившийся ток находим комплексным методом.

3. Находим свободную составляющую.

3.1. Определение общего вида свободной составляющей смотри в примере 1.

3.2. Определяем постоянную интегрирования.

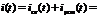
По первому закону коммутации  имеем ток в цепи при t=0₊ равным 0. Тогда ,

.

4. Записываем ответ и строим график:

Рис. 1.7.

Здесь следует заметить, что интенсивность переходного процесса зависит ещё и от фазы коммутации. Для параметров, приведённых на графике имеет место близость к максимально возможному переходному процессу при фазе коммутации Y®180^о. При слабом затухании с увеличением постоянной времени ( ) угол сопротивления j®90^о, тогда при Y®180^о будет иметь место максимальная интенсивность переходного процесса и ток дросселя может достигать ударного значения, равного удвоенной амплитуде установившейся величины.

32. Алгоритм расчета переходного процесса классическим методом в цепи второго порядка на примере подключения R-L-C-цепи к источнику постоянного напряжения.

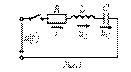
Рассмотрим два случая:

а) ;

б) .

Согласно изложенной в предыдущей лекции методике расчета переходных процессов классическим методом для напряжения на конденсаторе в цепи на рис. 3 можно записать

.

(1)

Тогда для первого случая принужденная составляющая этого напряжения

.

(2)

Характеристическое уравнение цепи

,

решая которое, получаем

.

В зависимости от соотношения параметров цепи возможны три типа корней и соответственно три варианта выражения для свободной составляющей:

1. 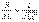или , где - критическое сопротивление контура, меньше которого свободный процесс носит колебательный характер.

В этом случае

.

(3)

2. 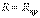- предельный случай апериодического режима.

В этом случае и

.

(4)

3. - периодический (колебательный) характер переходного процесса.

В этом случае и

,

(5)

где - коэффициент затухания; - угловая частота собственных колебаний; - период собственных колебаний.

Для апериодического характера переходного процесса после подстановки (2) и (3) в соотношение (1) можно записать

.

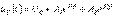Для нахождения постоянных интегрирования, учитывая, что в общем случае и в соответствии с первым законом коммутации 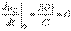, запишем для t=0 два уравнения:

решая которые, получим

; .

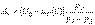Таким образом,

.

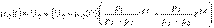Тогда ток в цепи

и напряжение на катушке индуктивности

.

На рис. 4 представлены качественные кривые , и , соответствующие апериодическому переходному процессу при .

Для критического режима на основании (2) и (4) можно записать

.

При

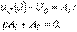
Таким образом

и

.

Для колебательного переходного процесса в соответствии с (2) и (5) имеем

.

Для нахождения постоянных интегрирования запишем

откуда и .

Тогда

.

На рис. 5представлены качественные кривые и , соответствующие колебательному переходному процессу при .

При подключении R-L-C-цепи к источнику синусоидального напряжения для нахождения принужденных составляющих тока в цепи и напряжения на конденсаторе следует воспользоваться символическим методом расчета, в соответствии с которым

и

,

где ; ; .

Таким образом,

и .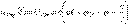

 

Здесь также возможны три режима:

1. ;	2.	3.

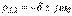
Наибольший интерес представляет третий режим, связанный с появлением во время переходного процесса собственных колебаний с частотой . При этом возможны, в зависимости от соотношения частот собственных колебаний и напряжения источника, три характерные варианта: 1 - ; 2 - ; 3 - , - которые представлены на рис. 6,а…6,в соответственно.

 

---

Дата добавления: 2018-08-06; просмотров: 618; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!
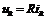
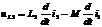
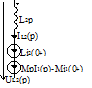
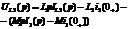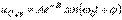