Включение электрической цепи на напряжение произвольной формы. Интеграл Дюамеля.
Пусть произвольный пассивный двухполюсник подключен к источнику напряжения, кривая изменения которого дана на рис. 5.18.
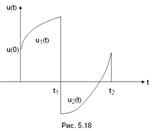
Решение:
Для вычисления тока определим переходную функцию h(t):
0< t< t1: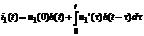 
.
Для учета скачка напряжения в точке t = t1 будем считать, что в этот момент к двухполюснику прикладывается отрицательное постоянное напряжение U = u2(t1) – u1(t1). Кроме того, учтем составляющие тока от начального скачка напряжения u1(0) и от элементарных скачков напряжения, определяемого кривой u1(t) и действующего от t=0 до t=t1. В результате получим:
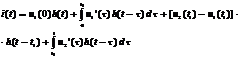
Для промежутка t2 < t < ¥ включается постоянное напряжение u = – u2(t2).
В итоге:
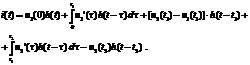
При подключении активного двухполюсного элемента к источнику напряжения, расчет проводится по принципу наложения.
Расчет с помощью интеграла Дюамеля проводят в 4 этапа:
1) Определение переходной функции h(t) для исследуемой цепи.
2) Определение h(t – t). С этой целью в функции h(t) заменяют t на (t – t).
3) Определение u’(t). Для этого находят производную от заданного напряжения u(t) по времени t, и в полученном выражении заменяют t на t.
4) Подстановка найденных на этапах 1, 2, 3 функций в формулу интеграла Дюамеля, интегрирование по переменной t и подстановка пределов.
Таким образом, если определена характеристика h(t), то при помощи интеграла Дюамеля можно определить реакцию системы при любой форме внешних воздействий.
|
|
|
Возникновение переходных процессов и законы коммутации.
В электрических цепях могут происходить события, приводящие к изменениям параметров или в топологии схемы. Такие изменения называются коммутациями. Примером коммутации могут быть:
· подключение (отключение) источника;
· короткое замыкание в какой-либо ветви;
· резкое изменение амплитуды или фазы источника.
На схемах для обозначения коммутации используют ключевой элемент с указанием стрелочкой вида коммутации (замыкание, размыкание) и момента времени.
Ключ считается идеальным элементом. Сопротивление ключа в открытом состоянии принимается равным нулю, а закрытом – бесконечности. Время коммутации есть бесконечно малая величина, то есть переход из одного состояния в другое происходит мгновенно.
Момент коммутации является границей между, так называемыми, до коммутационным (предшествующим) и переходным процессами (ПП). Теоретически переходный процесс длится бесконечно долго, но на практике это время считают конечным в силу затухающего характера переходного процесса. Во время переходного процесса электрическая величина стремится к некоторому установившемуся значению, по достижению которого с точностью до 99%, переходный процесс считают закончившимся. Дальнейшее состояние цепи называют установившимся процессом.
|
|
|
Рис. 1.1
Учет переходных процессов при проектировании и эксплуатации электротехнических устройств, как правило, обязателен. Например, в момент пуска двигателя в его обмотках могут возникать пусковые токи в несколько раз превышающие номинальные токи. Возможны в цепях и коммутационные перенапряжения, способные вызвать пробой изоляции, и как следствие, короткое замыкание.
Расчет переходных процессов основывается на решении (интегрировании) дифференциального уравнения, которым искомая величина (ток, напряжение, потокосцепление, заряд) связана с независимой переменной t – временем. Это уравнение получается из системы интегро-дифференциальных уравнений, которыми можно описать цепь по законам Кирхгофа. Оно называется линейным обыкновенным неоднородным дифференциальным уравнением (ОДУ) n-го порядка с постоянными коэффициентами вида
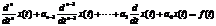(1.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) (1.2), которым удовлетворяют постоянные интегрирования:
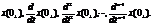(1.2)
|
|
|
Из теории дифференциальных уравнений мы знаем, что решением уравнения (1.1) является сумма его частного решения для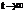 
и общего решения однородного дифференциального уравнения вида 
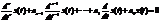(1.3)
Частное решение уравнения (1.1) называют установившейся или “принуждённой” составляющей, а решение уравнения (1.3) называют свободной составляющей
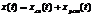(1.4)
Ток свободной составляющей переходного процесса обусловлен разницей энергий реактивных элементов до коммутации и в установившемся режиме. Ток принужденной составляющей обусловлен действием источников в цепи после коммутации.
I закон коммутации:
Ток через индуктивность непосредственно до коммутации iL(0–) равен току через туже индуктивность непосредственно после коммутации: iL(0–) = iL(0+).
II закон коммутации: uc(0–) = uc(0+).
В общем случае задача анализа переходных процессов заключается в определении мгновенных значений токов или напряжений всех или части ветвей электрической цепи в произвольный момент времени после коммутации и может быть сведена к решению дифференциального уравнения цепи при t>0.
25. Операторный метод расчета переходных процессов. Рассмотреть включение цепи R-L на постоянное напряжение операторным методом.
|
|
|
ОПЕРАТОРНЫЙ МЕТОД РАСЧЁТА ПЕРЕХОДНЫХ ПРОЦЕССОВ.
Электрическая величина в цепи, содержащей реактивные элементы может быть описана обыкновенным линейным дифференциальным уравнением n–ого порядка с постоянными коэффициентами вида
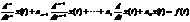(2.1)
Для его однозначного разрешения должны быть определены n начальных условий (НУ) 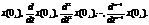(2.2):
(2.2)
Кроме классического метода решения этого уравнения существует операторный метод. Суть операторного метода заключается в применении к уравнению (2.1) преобразования Лапласа: 
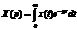, где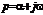 
. (2.3)
Принято говорить так, что над оригиналом x(t) - функцией действительного переменного t произведена операция отображения в область комплексного переменного p. X(p)-изображение функции x(t). С целью более простой записи, в место выражения (2.3), используют специальные символы: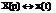 
или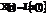 
. Так, например, если применить формулу (2.3) к уравнению (2.1), то получим алгебраическое уравнение в области изображений
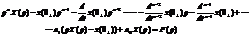(2.4)
Выражая из (2.4) изображение искомой величины мы получим дробно-рациональную функцию равную отношению полиномов
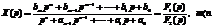(2.5)
Решение уравнения (2.1) находится путём вычисления обратного преобразования Лапласа над отношением полиномов (2.5) по формуле
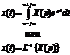
Дата добавления: 2018-08-06; просмотров: 273; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!