Высокочастотные реактивные фильтры.

Схема простейшего высокочастотного фильтраприведена на рис. 3,а.

Для данного фильтра коэффициенты четырехполюсника определяются выражениями

;

(9)

 

;

(10)

 

.

(11)

Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому на основании (9)

.

Данному неравенству удовлетворяет диапазон изменения частот

.

(12)

Характеристическое сопротивление фильтра

,

(13)

 

изменяясь в пределах от нуля до с ростом частоты, остается вещественным. Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с нагрузкой во всей полосе пропускания практически невозможно, реально фильтр работает с в ограниченном диапазоне частот.

Вне области пропускания частот определяется из уравнения

(14)

при . Плавное изменение коэффициента затухания в соответствии с (14) показывает, что в полосе задерживания фильтр не является идеальным.

Качественный вид зависимостей и для низкочастотного фильтра представлен на рис. 4.

 

Следует отметить, что другим примером простейшего высокочастотного фильтра может служить П-образный четырехполюсник на рис. 3,б.

Низкочастотные реактивные фильтры.

Рассмотрим схему простейшего низкочастотного фильтра,представленную на рис. 1,а.

Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы замещения определяется соотношениями (см. лекцию № 14)

или конкретно для фильтра на рис. 1,а

;

(2)

 

;

(3)

 

.

(4)

Из уравнений четырехполюсника, записанных с использованием гиперболических функций (см. лекцию № 14), вытекает, что

.

Однако в соответствии с (2) - вещественная переменная, а следовательно,

.

(5)

Поскольку в полосе пропускания частот коэффициент затухания , то на основании (5) .

Так как пределы изменения : , - то границы полосы пропускания определяются неравенством

,

которому удовлетворяют частоты, лежащие в диапазоне

.

(6)

Для характеристического сопротивления фильтра на основании (3) и (4) имеем

.

(7)

Анализ соотношения (7) показывает, что с ростом частоты w в пределах, определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением, равным характеристическому, его входное сопротивление также будет равно , то, вследствие вещественности , можно сделать заключение, что фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших , как это следует из (7), характеристическое сопротивление приобретает индуктивный характер.

На рис. 2 приведены качественные зависимости и .

Следует отметить, что вне полосы пропускания . Действительно, поскольку коэффициент А – вещественный, то всегда должно удовлетворяться равенство

.

(8)

Так как вне полосы прозрачности , то соотношение (8) может выполняться только при .

В полосе задерживания коэффициент затухания определяется из уравнения (5) при 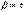. Существенным при этом является факт постепенного нарастания , т.е. в полосе затухания фильтр не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно сделать и для полосы прозрачности, поскольку обеспечить практически согласованный режим работы фильтра во всей полосе прозрачности невозможно, а следовательно, в полосе пропускания коэффициент затухания будет отличен от нуля.

17. Пассивные RC-фильтры. Коэффициенты передачи для низкочастотных и высокочастотных фильтров.

18. Активный низкочастотный RC-фильтр.

Активный фильтр нижних частот 1-го порядка c RC-цепью обратной связи показан на рис.2.4. Получим передаточную функцию этого фильтра. Обозначим Z₁=R₁ и эквивалентное сопротивление R₂C₁- цепи Z₂=R₂/ (1+jwC₁R₂). Сопротивления Z₁ и  Z₂ - это элементы цепи параллельной отрицательной обратной связи по напряжению. Будем считать, что ток утечки между точкой N и землей отсутствует, а входное сопротивление усилителя бесконечно велико. Тогда ток входного сигнала будет протекать только через элементы цепи обратной связи Z₁ и Z₂ , т. е. 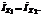 Если учесть, что  то передаточная функция такого фильтра будет иметь вид:

Если собственный коэффициент усиления велик K>>1, то потенциал точки N близок к нулю, и передаточная функция фильтра будет определяться только значениями элементов Z₁ и Z₂ цепи обратной связи:

где K₀ = - R₂ /R₁ , a₁=w_сR₂C₁.

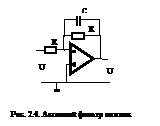
Для расчета схемы необходимо задать ча­стоту среза w_с, коэффициент передачи постоянного сигнала K₀ = - R₂ /R₁ (для этой схемы он должен быть задан со знаком минус) и ем­кость конденсатора С₁ . Приравняв коэф­фициенты полученной передаточной функ­ции коэффициентам выражения (2.1), по­лучим: R₂=a₁/w_cC₁ , R₁= - R₂ /K₀ .

Чтобы получить передаточную функцию фильтра верхних ча­стот первого порядка, необходимо в выражении (2.1) вели­чину p заменить на 1/p. Тогда

                 

Колебательный разряд конденсатора на катушку индуктивности. Апериодический разряд конденсатора на катушку индуктивности. Предельный апериодический разряд конденсатора на катушку индуктивности.

Одна из классических задач расчета переходных процессов — анализ разряда конденсатора на цепь с последовательным соединением резистора и катушки (рис. 15.8).

Рис. 15.8

Запишем уравнения переходного процесса в контуре Исключая из приведенной системы uC, придем к дифференциальному уравнению 2-го порядка относительно тока

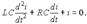
Характеристическое уравнение последовательного колебательного контура

(15.1)

имеет корни

которые в зависимости от соотношений между параметрами цепи могут быть:
1) вещественными различными (R > 2ЦL/C);
2) вещественными равными (R = 2ЦL/C);
3) комплексно-сопряженными (R < 2ЦL/C).

В первых двух случаях переходный процесс носит апериодический характер: разрядный ток не изменяет направления в течение всего процесса; в третьем случае процесс разряда колебательный.

При различных корнях (первый и третий случаи) общее решение однородного дифференциального уравнения можно записать в виде

Для определения двух постоянных интегрирования используем два начальных условия, вытекающих из условия непрерывности обеих переменных состояния в момент коммутации: i(0) = 0; u_C(0) = U₀. Из второго уравнения исходной системы можно найти значение производной di/dt в момент времени после коммутации. При t = + 0 di/dt = – U₀/L. Из общего решения для значения тока и его производной при подстановке получим систему для определения постоянных интегрирования:

,

решение которой приводит к значениям постоянных

и позволяет записать выражение для тока, удовлетворяющее начальным условиям:

.

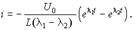Напряжение u_L имеет общее выражение

а для напряжения на конденсаторе u_C получим из второго уравнения исходной системы

При его преобразовании учтем, что из характеристического уравнения по теореме Виета следует l₁ + l₂ = – R/L. Это позволяет привести последнее выражение к виду

Ход разряда конденсатора существенно зависит от вида корней характеристического уравнения.

1. Апериодический разряд наблюдается при вещественных корнях l_{1, 2}, что имеет место при соотношении между параметрами цепи R > 2ЦL/C.

Пусть l₁ — меньший по абсолютному значению корень, к которому в формуле для корней относится знак “плюс” перед радикалом. При этом разность l₁ – l₂ в знаменателе выражения для тока положительная. Разность экспонент e^l1^t – e^l2^t также положительна, поскольку e^l1^t убывает медленнее, чем e^l2^t. Поэтому ток разряда сохраняет неизменное направление, противоположное направлению при заряде конденсатора. Поскольку i(0) = 0, в начале процесса — на фронте импульса — ток нарастает по абсолютному значению, а затем уменьшается (рис. 15.9).

Рис. 15.9

Начальная скорость нарастания тока di/dt(0) = |U₀/L| определяется значением индуктивности L. С ее уменьшением длительность фронта импульса сокращается, а абсолютное значение максимума i_max возрастает. Напряжение на индуктивности нарастает от значения – U₀ при t = 0, переходит через нуль в момент t_max достижения током максимального значения и изменяет знак. Анализ зависимости i(t) на экстремум показывает, что t_max = . Напряжение на конденсаторе u_C имеет в течение всего процесса монотонный спадающий характер. Сначала его спад происходит медленно, далее в окрестности максимума тока убывание u_C ускоряется, а затем вновь замедляется. Из условия баланса напряжений в контуре u_C = – (Ri + L di/dt) легко установить связи между напряжениями на отдельных элементах и током в контуре. Так, в начальный момент разряда u_C = U₀; u_L = – U₀; i = 0. В момент максимума тока t_max u_C = – Ri, а u_L = 0; в течение всего процесса имеем u_C > | u_L|, так как Ri < 0.

2. Критический разряд.Характер всех рассмотренных зависимостей (при кратных корнях l₁ = l₂ = l = – R/2L) сохраняется. Решение для тока получим из общей формулы, раскрывая неопределенность при l₁ = l₂ = l

Для напряжений на индуктивности и емкости найдем:

Из приведенных выражений следует, что, как и при апериодическом разряде, значение тока в течение всего процесса отрицательно, напряжение u_L изменяет знак в момент максимума тока t_max = – 1/l = 2L/R = , а напряжение на емкости имеет монотонный падающий характер.

3. Колебательный разряд наблюдается при комплексно-сопряженных корнях характеристического уравнения (при R < 2ЦL/C или добротность контура Q > 0,5). Выражая корни через их вещественные и мнимые части l_{1, 2} = – d ± jw' (d = – R/2L; w' = ), преобразуем общие соотношения для i, u_L и u_C:

В этих преобразованиях использованы формулы Эйлера. Соотношения показывают, что все три переменные имеют при разряде колебательный характер, периодически изменяя знак. Период колебаний T определяется из условия изменения аргумента тригонометрических функций на 2p: 2p = w'T, откуда

Период колебаний в контуре без потерь равен T₀ = 2pЦLC. Затухание колебаний по амплитуде, определяемое экспоненциальными множителями e^{– dt}, зависит от соотношения параметров контура. Обычно эта величина количественно характеризуется декрементом колебания D, равным отношению двух последующих амплитуд одного знака, отстоящих друг от друга на период D = e^{– dt}/e^{– d(t+T)} = e^dT. Вводится также понятие логарифмического декремента колебаний ln D = dT. У высокодобротного контура затухание имеет малое значение, вычитаемое в подкоренном выражении для периода T также мало, и T » T₀ = 2pЦLC. При этом ln D = (R/2L) 2pЦL/C = pR/ЦL/C = pd = p/Q, где d = R/ЦL/C = 1/Q – затухание контура. Этим определяется смысл понятия затухания, которое при сделанных допущениях, практически выполняющихся при d < 0,2, пропорционально логарифмическому декременту колебаний. При этих значениях параметров, что соответствует D < 2, частота собственных колебаний контура w' практически равна его резонансной частоте w' » w₀ = 1/ЦLC. Зависимости i, u_L и u_C(t) для D = 2 изображены на рис. 15.10.

Рис. 15.10

Начальная часть процесса (при t < T/4) имеет характер, сходный с начальной частью апериодического разряда. Однако теперь к моменту максимума тока t » T/4 катушка успевает накопить бóльшую часть энергии, первоначально запасенной в конденсаторе, который к этому времени уже почти разряжен. Далее, по мере спада тока, во второй четверти периода (T/4 < t < T/2) конденсатор перезаряжается, но напряжение на нем изменяет полярность на противоположную, а накопленная в катушке энергия вновь возвращается к конденсатору. Этот периодический обмен энергией продолжается и в последующие фазы разряда, но его интенсивность постепенно ослабевает, так как в течение каждого цикла перезарядки часть энергии рассеивается в виде тепла в сопротивлении контура R.

---

Дата добавления: 2018-08-06; просмотров: 433; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!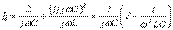