Устойчивость дискретных систем. Пример анализа.
Устойчивость дискретных систем
Для определения устойчивости дискретных систем используют алгебраические и частотные критерии.
Алгебраический критерий: проверяется система неравенств, связывающих коэффициенты характеристического уравнения:
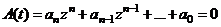
В принципе его можно решить и определить корни. Тогда можно использовать следующие условия: корни характеристического уравнения устойчивых систем расположены в левой полуплоскости комплексной плоскости S. Когда мы переходим к z-плоскости, это условие соответствует тому, что все корни z должны быть меньше 1.
Характеристическое уравнение составляется путем приравнивания к нулю знаменателя.
,
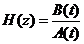но этот путь – длинный.
Существуют критерии, заключенные в проверке системы неравенств:
Если n = 1: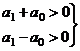 
Если n = 2: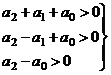 
Если n = 3: составляются 5 неравенств
Если n > 3: Данные находятся в справочниках.
Частотные критерии:
Критерий Найквиста – строим годограф комплексной плоскости разомкнутой системы и проверяем охват точки (-1; j0). Если годограф не охватывает эту точку, то система устойчива.
При исследовании дискретных систем, при построении годографа, частоту изменяют от 0 до 2π/Т.
Проанализируем устойчивость схемы:
,
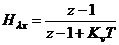Характеристическое уравнение: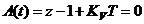 
Общий вид: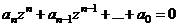 
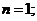
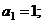
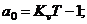
Условие устойчивости для систем с условием n = 1:
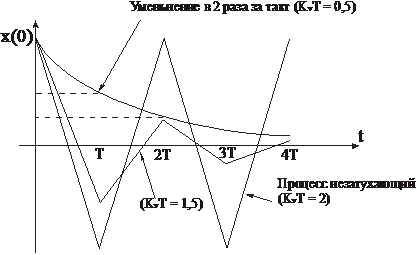
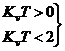Т.о. накладываются ограничения на период дискретизации и на Kv.
|
|
|
Непрерывная система с одним интегратором не имеет таких ограничений.
Пусть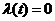 
при t = 0, а на выходе интегратора есть какое-то напряжение U, соответственно в момент времени t = 0 получим:
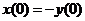– на входе интегратора;
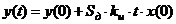– на выходе интегратора.
Соответственно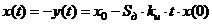 
, а через такт, при t = T:
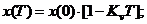
Графически:
Уменьшение в 2 раза за такт (KvT = 0,5).
Анализ детерминированных процессов в дискретной системе.
Анализ детерминированных процессов в дискретных системах.
Задачей анализа является определение xуст или зависимости выходной величины от входной. Анализ можно производить с помощью Z-преобразований, если мы имеем:
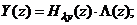
то нам необходимо определить оригинал по z-изображению выходной величины.
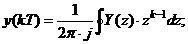
Вычислим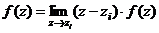 
для простого полюса.
Вычислим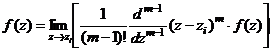 
для полюса порядка m.
С помощью этих выражений мы можем определить оригинал.
Если нас интересует установившееся значение величины, мы можем использовать теорему о предельном значении оригинала:
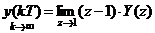
В некоторых случаях можно использовать таблицы, если выражение z-изображения простое или разложив его можно разложить на простые.
Определим значение ошибки для системы, имеющие в своем составе интегратор.
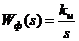
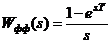
Пусть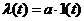 
. Т.к.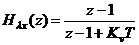 
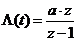= по таблицам.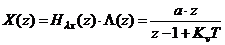 
хуст = 0 (астатизм первого порядка):
|
|
|
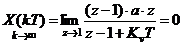
Характер переходного процесса:
Используем теорему обращения:
;
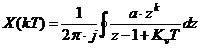подынтегральное выражение имеет 1 полюс: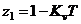 
, тогда:
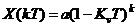
Подставляя последовательно k, можем исследовать характер переходного процесса.
Можем также использовать разностное уравнение для определения выходной величины: если его порядок высокий, используют вычислительное свойство, если нет, то можно действовать пошагово:
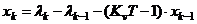
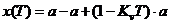
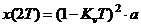
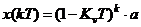
Дата добавления: 2018-08-06; просмотров: 506; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!