Математические методы описания дискретных систем. Z-преобразование и его свойства.
1. Z – преобразование и его свойства.
На входе дискретной системы действует непрерывный процесс. Но мы получаем информацию только в тактовых точках. Соответственно 
нас интересует только в тактовых точках 
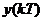. Поэтому для анализа таких систем используются дискретные методы: 
; 
; ДУ преобразуем в разностное уравнение; используются дискретное преобразование Фурье и Лапласа.
Дискретное преобразование Лапласа:
, где 
- изображение; 
- оригинал.
Для анализа неудобно, т.к. изображение является трансцендентной функцией от изменения (переменной). Поэтому используем Z – преобразование, путем замены:
, тогда:
;
свойства Z – преобразования
1. Теорема обращения: 
;
2. 
;
3. 
;
4. Теорема о конечном значении оригинала:
;
5. Теорема о начальном значении оригинала:
;
6. Теорема свертки оригиналов:
;
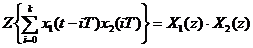7. Теорема запаздывания:
;
при ненулевых начальных условиях 
.
если начальные условия нулевые, то:
;
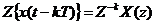8. 
;
9. 
, где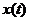 
- непрерывная величина.
(8) и (9) можно обобщить:
Передаточная функция дискретной системы. Разностные уравнения.
Полагая 
:
Передаточная функция дискретной замкнутой системы:
; 
;
выразим 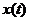через 
и .
где 
; 
;
выразив через 
определим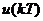 
: 
;
если подать на формирующий фильтр последовательность 
- функций или на фильтр с ПФ 
мы получим на выходе отклик, равный сумме импульсных характеристик.
, где 
- импульсная характеристика.
Разностные уравнения
|
|
|
Разностные уравнения определяют связь между значениями выходной и входной величин в тактовых точках через дискретизации.
Чтобы составить РУ надо представить дискретную передаточную функцию в следующем виде:
(1);
Если 
- значение выходной величины, а 
- входной в виде Z – изображения, то связь между ними определяется выражением:
(2);
подставим (1) в (2):
(3);
применим к левой и правой частям теорему обращения. С учетом теоремы запаздывание оригинала мы можем записать:
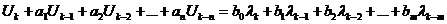(4);
где 
; 
.
Из (4) можно определить значения оригинала в тактовых точках.
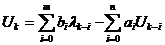(5).
Таким образом мы получили разностное уравнение которое может определить значение величины в тактовых точках. Значение выходной величины зависит как от значения входной величины, так и от значения выходной величины в предыдущих тактовых точках.
Операторный и комплексный коэффициенты передачи дискретной системы.
Операторный коэффициент передачи дискретной системы
Чтобы его найти существует оператор запаздывания – С.
|
|
|
Воздействие его на величину приводит к запаздыванию на такт:
…………………………
.
Чтобы перейти от дискретной ПФ к операторному коэффициенту передачи, необходимо сделать замену:
;
в результате мы получим:
;тогда 
;
Комплексный коэффициент передачи дискретной системы
Комплексный коэффициент передачи дискретной системы можно получить из ПФ дискретной системы путем замены: 
.
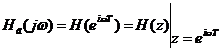Рассмотрим физический смысл комплексного коэффициента передачи:
Если мы на вход дискретной системы подадим гармонический сигнал, то реакция системы на него будет такого вида:
- искаженный гармонический сигнал в тактовых точках ошибки нет (выходной сигнал равен соответствующему значению гармонического сигнала). А в промежутках ошибка есть. Поэтому комплексный КП есть величина периодическая. Период 
. Это легко показать, если взять два воздействия:
и 
; текущее время 
, т.е. в такт Т.
;
Т.о. 
Дата добавления: 2018-08-06; просмотров: 340; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!