Статистический анализ уравнения регрессии
Для того чтобы установить, соответствует ли выбранная регрессионная модель экспериментальным данным, используют основное уравнение дисперсионного анализа, записанное в виде:
,
где: 
общая сумма квадратов отклонений значений Y от общей средней, определяемая формулой:
,
сумма квадратов отклонений, обусловленная регрессией, определяемая формулой:
,
остаточная сумма квадратов, определяемая формулой:
.
В случае не сгруппированной выборки приведенные формулы для сумм несколько упрощаются и принимают вид:
Приведенные формулы позволяют найти соответствующие исправленные дисперсии:
,
где: 
число групп в корреляционной таблице или число оцениваемых параметров в не сгруппированной выборке, а n – число наблюдений.
Для заданного уровня значимости α и количеств степеней свободы 
по таблицам находим критическое значение 
критерия Фишера-Снедекора. Если для наблюдаемого значения критерия выполняется неравенство:
,
то уравнение регрессии считается значимым или соответствующим экспериментальным данным на уровне значимости α.
Воздействие неучтенных случайных факторов в линейной модели регрессии определяется остаточной дисперсией, оценкой которой является выборочная остаточная дисперсия 
.
ПРИМЕР: Для зависимости Y от Х, заданной корреляционной таблицей 2.1 подраздела 2.5.1, найти оценки параметров уравнения линейной регрессии, остаточную дисперсию, а также оценить значимость найденного уравнения регрессии при 
.
|
|
|
Воспользуемся результатами, полученными в примерах подразделов 2.5.1 ÷ 2.5.4:
С учетом формулы искомое уравнение регрессии можно записать в виде:
или: 
,
но тогда: 
и 
.
Для выяснения значимости найденного уравнения регрессии вычислим суммы 
и 
, для чего составим и заполним расчетную таблицу:
| 
| 
| 
| 
|
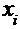
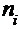
| 12,5 | 20,62 | 1 | 7,73 | 0,0144 |
| 17,5 | 21,82 | 3 | 7,49 | 0,6672 |
| 22,5 | 23,04 | 5 | 0,65 | 1,2180 |
| 27,5 | 24,24 | 11 | 7,76 | 2,1836 |
| - | 20 | 23,63 | 4,0832 |
Таким образом, получены значения: 
и 
. В рассматриваемом случае 
и 
, поэтому найдем соответствующие исправленные дисперсии:
,
а также наблюдаемое значение критерия Фишера-Снедекора:
.
По таблицам критических точек распределения Фишера-Снедекора для уровня значимости и чисел степеней свободы: 
найдем критическую точку 
. Поскольку 
, полученное уравнение регрессии значимо, а остаточная (необъясненная) дисперсия равна: 
.
Рекомендуемая литература по теме 2.5:[1 ÷ 4, 6].
ВОПРОСЫ для самопроверки знаний по теме 2.5:
1. Какое различие между функциональной, стохастической и корреляционной зависимостями?
|
|
|
2. Что записывается в последних строке и столбце корреляционной таблицы?
3. Какой величиной характеризуется степень линейной зависимости между случайными величинами?
____________________________________________________________
4. Какой величиной характеризуется степень любой зависимости между случайными величинами?
____________________________________________________________
5. Какой коэффициент стоит при независимой переменной в уравнении линейной регрессии?
6. С помощью какого критерия проверяется значимость линейного уравнения регрессии?
ЛИТЕРАТУРА
1. Налимов В.Н. Теория вероятностей и математическая статистика для экономистов: Учебное пособие – М.: «Весть», 2007.
2. Болдин К.В. и др. Основы теории вероятностей и математической статистики: Учебник. – М.: Флинта, 2010.
3. Попов А.М., Сотников В.Н. Теория вероятностей и математическая статистика: Учебник. – М.: Юрайт, 2011.
4. Геворкян П.С. и др. Теория вероятностей и математическая статистика: Учебник. – М.: Экономика, 2012.
5. Налимов В.Н. Основы теории и методы решения дифференциальных и разностных уравнений для экономистов: Учебное пособие. – М.: Издание ИМЭС, 2013.
|
|
|
6. Налимов В.Н. Основы математического анализа для экономистов: Учебное пособие. – М.: Издание ИМЭС, 2013.
Дата добавления: 2018-06-01; просмотров: 449; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!