Числовые характеристики вариационных рядов
Основной числовой характеристикой вариационного ряда является его средняя арифметическая, называемая также выборочной средней.
Для дискретного вариационного ряда выборочная средняя вычисляется по формуле:
|
Для интервального ряда за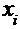 
принимают середину 
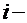го интервала, а выборочную среднюю вычисляют по формуле:
|
Вариационным размахом называется число 
Выборочной дисперсией называется средняя арифметическая квадратов отклонений вариант от их выборочной средней:
|
Выборочная дисперсия обладает теми же свойствами, что и дисперсия случайной величины.
Пусть значения выборки разбиты на k групп. Обозначим через 
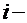количество различных вариант в ой группе, через 
частоту 
ой варианты в этой группе. Тогда 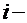ую группу можно записать в виде: 
, при этом значение 
повторяется 
раз. Обозначим через 
групповые средние:
Тогда групповые дисперсии 
будут равны:
Средняя арифметическая групповых дисперсий будет равна:
Межгрупповая дисперсия равна:
Правилом сложения дисперсий называется равенство:
Еще одной мерой вариации признака является выборочное среднее квадратическое отклонение, которое определяется как корень квадратный из выборочной дисперсии.
При статистическом анализе рассматривается также коэффициент вариации, равный процентному отношению выборочного среднего квадратического отклонения к выборочной средней:
|
|
|
ПРИМЕР:В таблице приведены данные об урожайности ржи на различных участках поля:
| Урожайность ржи, ц/га | [9-12] | [12-15] | [15-18] | [18-21] | [21-24] | [24-27] |
| Доля участка в общей площади, % | 6 | 12 | 33 | 22 | 19 | 8 |
Найти размах вариации, выборочную дисперсию и коэффициент вариации признака Х – урожайности ржи.
Используя приведенные выше формулы, последовательно найдем:
Таким образом, выборочная дисперсия равна 15,3, следовательно выборочное среднее квадратическое отклонение равно 
и коэффициент вариации: 
Рекомендуемая литература по теме 2.1: [1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 2.1:
1. В чем различие между выборочной и генеральной совокупностями?
2. Как можно из частоты варианты получить ее относительную частоту?
3. Какие величины составляют вариационный ряд?
4. Как связаны значения эмпирической функции распределения с накопленными частотами?
5. Как определяются выборочные средние для дискретного и интервального вариационных рядов?
6. Может ли выборочная дисперсия быть отрицательной?
|
|
|
____________________________________________________________
Тема 2.2. Оценка параметров генеральной совокупности
Точечные оценки параметров
Пусть перед нами стоит задача изучения некоторого количественного признака Х в генеральной совокупности. Допустим, что каким-то образом нам удалось установить, какое именно распределение имеет изучаемый признак в генеральной совокупности. Возникает задача оценки (нахождения некоторых приближенных значений) неизвестных параметров этого распределения. Этими параметрами могут быть, например,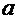 
и 
нормального распределения, или параметр 
распределения Пуассона. На практике о величине неизвестного параметра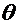 
можно судить по выборке объема n, извлеченной из генеральной совокупности, т.е. 
.
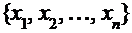Оценкой 
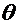параметра называется любая функция от значений выборки 
, т.е. статистика.
Заметим, что под самим параметром 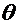понимается его истинное значение в генеральной совокупности, являющееся постоянным (неслучайным) числом. Статистику можно рассматривать как функцию от случайных величин 
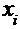таких, что значение есть реализация случайной величины 
:
Очевидно, что статистику следует выбирать таким образом, чтобы ее значения как можно точнее оценивали значение неизвестного параметра .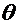
|
|
|
Несмещенной называется оценка параметра 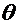, если ее математическое ожидание равно значению этого параметра, т.е.:
|
Если это требование не выполняется, то оценка будет давать значение параметра с некоторым отклонением в ту или другую сторону. Для несмещенных оценок устраняется возможность появления систематических ошибок при оценке параметра .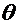
Эффективной называется оценка , которая при заданном объеме выборки имеет наименьшую возможную дисперсию:
Состоятельной называется оценка , которая при неограниченном увеличении объема выборки стремится по вероятности к оцениваемому параметру 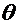, т.е. для любого 
выполняется:
Оценки называются точечными, т.к. они дают одно числовое значение параметра 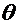(точку).
Пусть из генеральной совокупности Х извлечена повторная выборка со значениями признака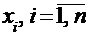 
. В качестве оценок для генеральной средней 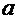и генеральной дисперсии 
рассмотрим выборочную среднюю 
и выборочную дисперсию 
.
Можно показать, что оценка для генеральной средней 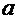является несмещенной, эффективной и состоятельной, а ее дисперсия равна:
В то же время, оценка для генеральной дисперсии является состоятельной, но смещенной. Поэтому на практике часто пользуются исправленной выборочной дисперсией 
, которая является несмещенной оценкой генеральной дисперсии и вычисляется по формуле:
|
|
|
Для бесповторной выборки оценки и также являются несмещенными и состоятельными, а дисперсия 
равна:
,
где 
объем генеральной совокупности. При неограниченном увеличении объема генеральной совокупности бесповторная выборка неотличима от повторной выборки.
Пусть генеральная совокупность содержит М элементов, обладающих некоторым признаком А.
Генеральной долей признака А называется величина 
, где объем генеральной совокупности.
Для генеральной доли р несмещенной и состоятельной оценкой будет являться выборочная доля 
, где 
число элементов выборки, обладающих признаком А.
Дисперсия выборочной доли в случае повторной выборки определяется по формуле:
,
а в случае бесповторной выборки – по формуле:
,
где: 
. Если 
, то повторная выборка практически не отличается от бесповторной, и приведенные формулы для дисперсии выборочной доли дают одинаковый результат.
В случае, когда р неизвестно, его заменяют выборочным значением 
.
ПРИМЕРЫ:
1. Из 1500 деталей отобрано 250, распределение которых по размеру задано таблицей:
| Размер детали | 7,8-8,0 | 8,0-8,2 | 8,2-8,4 | 8,4-8,6 | 8,6-8,8 | 8,8-9,0 |
| Количество | 5 | 20 | 80 | 95 | 40 | 10 |
Найти оценки и для среднего и дисперсии, а также дисперсию оценки для повторного и бесповторного отбора.
Используя соответствующие формулы, последовательно найдем:
Далее, для повторной выборки найдем:
а для бесповторной:
2. Выборочно обследовали партию кирпича, поступившего на стройку. Из 100 проб в 12 случаях кирпич оказался бракованным. Найти оценку доли бракованного кирпича и ее дисперсию.
По данным задачи имеем: 
. Далее найдем:
Дата добавления: 2018-06-01; просмотров: 1539; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!