Проверка гипотезы о равенстве средних значений
На практике часто встречаются ситуации, когда среднее значение данных одного эксперимента отличается от среднего значения данных другого, хотя условия эксперимента являются схожими. Тогда возникает вопрос, можно ли считать это расхождение незначимым, т.е. чисто случайным, или оно вызвано существенным различием двух генеральных совокупностей.
Пусть генеральные совокупности Х и Y распределены нормально, причем дисперсии их неизвестны, но есть веские основания полагать, что они равны, и требуется проверить нулевую гипотезу 
при конкурирующей гипотезе 
, по данным малых независимых выборок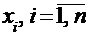 
и 
, извлеченных из этих совокупностей.
В рассматриваемом случае в качестве критерия принимается случайную величину:
,
где 
и 
- выборочные средние, а 
и 
- исправленные выборочные дисперсии. Доказано, что эта случайная величина при справедливости нулевой гипотезы имеет распределение Стьюдента с 
степенями свободы.
Исходя из вида конкурирующей гипотезы, будем строить двустороннюю критическую область. Поскольку распределение Стьюдента симметрично относительно нуля, нам достаточно найти правую критическую точку исходя из условия 
. Для ее отыскания пользуются таблицами критических точек распределения Стьюдента и данными по уровню значимости 
и числу степеней свободы .
По приведенной выше формуле рассчитывают наблюдаемое значение критерия 
и сравнивают его с найденной критической точкой. Если 
, то опытные данные не дают оснований отвергнуть нулевую гипотезу, если же 
, то нулевую гипотезу отвергают.
|
|
|
ПРИМЕР: По двум независимым малым выборкам с объемами 
и 
, соответственно, извлеченным из нормальных генеральных совокупностей Х и Y, найдены выборочные средние 
и исправленные выборочные дисперсии 
. При уровне значимости 
проверить нулевую гипотезу 
при конкурирующей гипотезе 
, если известно, что генеральные дисперсии в обеих совокупностях одинаковы.
Вычислим наблюдаемое значение критерия, подставив в формулу для него исходные данные задачи:
.
Исходя из вида конкурирующей гипотезы, выбираем двустороннюю критическую область и по таблицам критических точек распределения Стьюдента для уровня значимости 0,05 и числу степеней свободы 9 находим правую критическую точку: 
. Поскольку 
, нулевую гипотезу о равенстве генеральных средних отвергаем. Другими словами, выборочные средние различаются значимо.
Проверка гипотезы о равенстве генеральных дисперсий
На практике задача сравнения дисперсий возникает, когда требуется сравнить между собой точности приборов, инструментов, самих методов измерений и т.д. Очевидно, что предпочтительнее тот прибор, инструмент или метод, который обеспечивает наименьшее рассеяние результатов измерений, т.е. наименьшую дисперсию.
|
|
|
Пусть генеральные совокупности Х и Y распределены нормально. По независимым выборкам с объемами, соответственно равными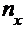 
и 
, извлеченными из этих совокупностей, найдены исправленные выборочные дисперсии и . Требуется при заданном уровне значимости проверить нулевую гипотезу о равенстве генеральных дисперсий 
при конкурирующей гипотезе 
.
В качестве критерия проверки нулевой гипотезы обычно выбирается случайная величина, равная отношению большей дисперсии к меньшей, т.е.:
,
которая при справедливости нулевой гипотезы имеет распределение Фишера-Снедекора со степенями свободы 
и 
, где 
объем выборки, по которой найдена большая дисперсия, а 
объем выборки, по которой найдена меньшая дисперсия.
Исходя из вида конкурирующей гипотезы, строят правостороннюю критическую область. Критическую точку находят по таблицам критических точек распределения Фишера-Снедекора по данным 
, т.е. 
. Находят наблюдаемое значение критерия 
и сравнивают его с критическим значением. Если 
, то нет оснований отвергнуть нулевую гипотезу, если же 
, то нулевую гипотезу отвергают.
|
|
|
ПРИМЕР: По двум независимым выборкам объемом 
и 
, извлеченным из нормальных генеральных совокупностей Х и Y, найдены исправленные выборочные дисперсии 
и 
. При уровне значимости проверить нулевую гипотезу , если конкурирующая гипотеза имеет вид: .
Найдем отношение большей исправленной дисперсии к меньшей, что и будет являться наблюдаемым значением критерия:
.
По таблицам критических точек распределения Фишера-Снедекора по уровню значимости и числам степеней свободы 
и 
найдем критическую точку для правосторонней критической области: 
. Поскольку , у нас нет оснований отвергнуть нулевую гипотезу.
Дата добавления: 2018-06-01; просмотров: 832; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!