Тема 2.1. Вариационные ряды и их характеристики
Генеральная и выборочная совокупности
Генеральной совокупностью называется совокупность объектов или наблюдений, все элементы которой подлежат изучению при статистическом анализе.
В математической статистике понятие генеральной совокупности часто отождествляют с понятием случайной величины (законом распределения вероятностей).
В зависимости от количества объектов генеральная совокупность может быть конечной или бесконечной.
Объемом генеральной совокупности называется число объектов (наблюдений).
Выборочной совокупностью или выборкой называется часть объектов генеральной совокупности, случайно отобранных из нее и предназначенных для исследования.
Объемом выборки называется число объектов (наблюдений) в нее входящих.
Сущность выборочного метода в математической статистике заключается в том, чтобы по определенной части генеральной совокупности (выборке) судить о ее свойствах в целом.
Выборочный метод является единственно возможным в случае бесконечной генеральной совокупности или когда исследование связано с уничтожением наблюдаемых объектов (например, исследование предельных режимов работы приборов, исследование воздействия вируса на подопытных животных и т.д.).
Для того чтобы по выборке можно было адекватно судить о случайной величине, выборка должна быть репрезентативной (представительной). Репрезентативность выборки обеспечивается объемом выборки и случайностью отбора ее элементов, т.е. все элементы генеральной совокупности должны иметь одинаковую вероятность попадания в выборку.
|
|
|
Существуют два способа образования выборки (отбора объектов из генеральной совокупности):
1. повторная выборка, когда каждый элемент, случайно отобранный и исследованный, возвращается в генеральную совокупность и может быть отобран повторно;
2. бесповторная выборка, когда элемент, случайно отобранный и исследованный, не возвращается в генеральную совокупность.
Вариационный ряд и его графические изображения
Пусть некоторый признак генеральной совокупности описывается случайной величиной Х. Если из генеральной совокупности извлечь выборку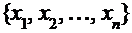 
объема n, то элементы выборки будут представлять собой значения случайной величины Х.
На начальном этапе статистической обработки производят ранжирование выборки, т.е. упорядочивание чисел 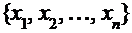по возрастанию.
Вариантами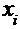 
называются различные элементы выборки.
Частотой варианты 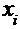называется число 
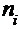, показывающее, сколько раз эта варианта встречается в выборке.
Относительной частотой или долей варианты 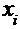в выборке объема n называется число 
.
|
|
|
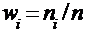Частоты и относительные частоты называются весами.
Пусть х некоторое число, тогда количество вариант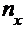 
, значения которых меньше х, называется накопленной частотой.
Отношение накопленной частоты к объему выборки называется накопленной относительной частотой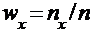 
.
Вариационным рядом называется ряд вариант, расположенных в порядке возрастания их значений, с соответствующими весами.
Дискретным называется вариационный ряд, представляющий собой выборку значений дискретной случайной величины. Обычно дискретный вариационный ряд записывают в виде таблицы:
| Варианты |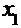 
| 
| … | 
|
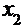
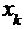
| Частоты |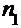 
| 
| … | 
|
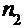
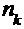
Непрерывным (интервальным) называется вариационный ряд, который представляет собой выборку значений непрерывной случайной величины.
Для построения интервального вариационного ряда разбивают множество значений вариант на полуинтервалы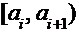 
, т.е. производят их группировку. Оптимальное количество интервалов k рекомендуется определять по формуле Стерджесса: 
При этом длина интервала будет равна: 
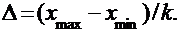Подсчитывая число значений, попавших в 
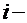ый полуинтервал, получим значения частот 
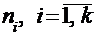. При этом, если варианта находится на границе интервала, ее причисляют к правому интервалу.
|
|
|
В результате получают интервальный ряд, который записывают в виде таблицы:
| Варианты |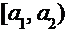 
| 
| … | 
|
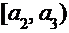
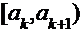
| Частоты |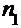
|
| … |
|
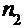
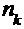
Для наглядности представления используют графические изображения вариационных рядов в виде полигона, гистограммы и кумуляты.
Полигон служит для изображения дискретного вариационного ряда и представляет собой ломаную, соединяющую точки с координатами 
. Для интервального ряда также строится полигон, только его ломаная соединяет точки 
, где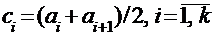 
.
Гистограмма служит только для представления интервальных вариационных рядов и имеет вид ступенчатой фигуры из прямоугольников с основаниями, равными длине интервалов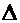 
, и высотами, равными частотам 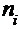соответствующих интервалов.
Кумулята представляет собой ломаную, соединяющую точки с координатами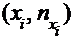 
для дискретного ряда, или точки с координатами 
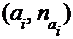для интервального ряда.
Эмпирической функцией распределения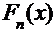 
называется функция, значение которой в точке х равно накопленной относительной частоте, т.е. 
.
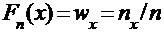Для интервального ряда указываются не конкретные значения вариант, а только их частоты на интервалах. В этом случае эмпирическая функция распределения будет определена только на концах интервалов, и ее можно изобразить ломаной, проходящей через точки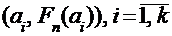 
.
|
|
|
Эмпирической плотностью распределения непрерывного вариационного ряда называется функция
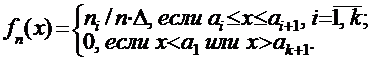
ПРИМЕРЫ:
1. В магазине за день продано 45 пар мужской обуви. Имеется выборка значений случайной величины Х – размера обуви:
39, 41, 40, 42, 41, 40, 42, 44, 40, 43, 42, 41, 43, 39, 42,
41, 42, 39, 41, 37, 43, 41, 38, 43, 42, 41, 40, 41, 38, 44,
40, 39, 41, 40, 42, 40, 41, 42, 40, 43, 38, 39, 41, 41, 42.
Построить дискретный вариационный ряд, полигон, кумуляту и эмпирическую функцию распределения.
Различные значения признака располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту. В результате вариационный ряд имеет вид:
|
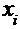
| 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 |
|
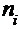
| 1 | 3 | 5 | 8 | 12 | 9 | 5 | 2 |
Полигон этого распределения изображен на рис. 2.1.
По данным вариационного ряда находим накопленные частоты и относительные частоты и заносим полученные значения в таблицу:
|
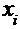
| 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
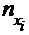
| 0 | 1 | 4 | 9 | 17 | 29 | 38 | 43 | 45 |
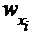
| 0 | 0,022 | 0,089 | 0,2 | 0,378 | 0,644 | 0,844 | 0,978 | 1 |
По данным полученной таблицы строим кумуляту (рис. 2.2) и эмпирическую функцию распределения (рис. 2.3).
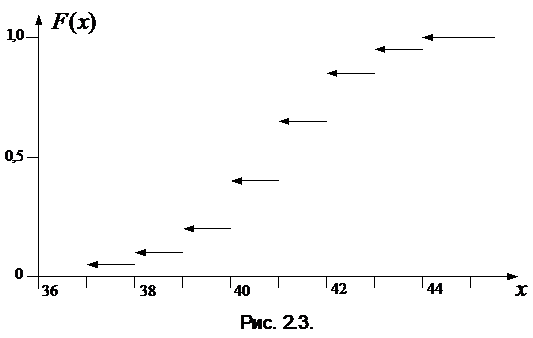
2. Результаты измерений отклонений от номинала диаметров 50 подшипников дали численные значения (в микронах):
-1,752 -0,291 -0,933 -0,450 0,512 -1,256 1,701 0,634 0,720 0,490
1,531 -0,433 1,409 1,730 -0,266 -0,058 0,248 -0,095 -1,488 -0,361
0,415 -1,382 0,129 -0,361 -0,087 -0,329 0,086 0,130 -0,244 -0,882
0,318 -1,087 0,899 1,028 -1,304 0,349 -0,293 -0,883 -0,056 0,757
-0,059 -0,539 -0,078 0,229 0,194 -1,084 0,318 0,367 -0,992 0,529.
Для данной выборки построить интервальный вариационный ряд, полигон, гистограмму, графики эмпирической функции распределения и эмпирической плотности распределения.
По данным выборки находим: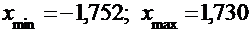 
. Разобьем множество значений на интервалы. Количество интервалов найдем по формуле Стерджесса: 
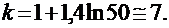Начало первого интервала 
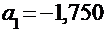, а конец последнего седьмого интервала 
. При этом варианту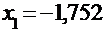 
отнесем в первый интервал. Длина интервалов будет равна:
.
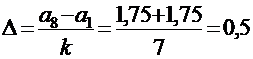Подсчитав число вариант, попадающих в каждый интервал, получим таблицу вариационного ряда:
| [ai, ai+1) | [-1,75; -1,25) | [-1,25; -0,75) | [-0,75; -0,25) | [-0,25; 0,25) | [0,25; 0,75) | [0,75; 1,25) | [1,25; 1,75) |
|
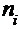
| 5 | 8 | 9 | 12 | 9 | 3 | 4 |
По данным таблицы строим полигон и гистограмму распределения (рис. 2.4).
Для построения эмпирической функции распределения вычислим относительные накопленные частоты и составим таблицу:
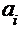
| -1,75 | -1,25 | -0,75 | -0,25 | 0,25 | 0,75 | 1,25 | 1,75 |
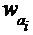
| 0 | 0,1 | 0,26 | 0,44 | 0,68 | 0,86 | 0,92 | 1 |
Найдем значения эмпирической плотности вероятности для каждого интервала по формуле: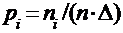 
и составим таблицу:
| [ai, ai+1) | [-1,75; -1,25) | [-1,25; -0,75) | [-0,75; -0,25) | [-0,25; 0,25) | [0,25; 0,75) | [0,75; 1,25) | [1,25; 1,75) |
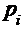
| 0,2 | 0,32 | 0,36 | 0,48 | 0,36 | 0,12 | 0,16 |
На рис. 2.5 изображена эмпирическая функция распределения, а на рис. 2.6 – эмпирическая плотность распределения.
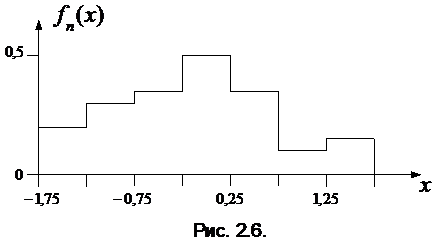
Дата добавления: 2018-06-01; просмотров: 831; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!