Независимые и зависимые случайные величины. Коэффициент корреляции
Независимыми называются случайные величины Х и Y, для которых совместная функция распределения 
равна произведению функций распределения 
и 
этих случайных величин, т.е.: 
Если случайные величины Х и Y независимы и имеют совместную плотность 
, то она будет равна произведению плотностей 
и 
этих величин: 
.
Коэффициентом корреляции двух случайных величин Х и Y называется число 
, определяемое формулой:
Свойства коэффициента корреляции
1. 
2. Если Х и Y независимы, то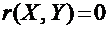 
.
3. Если 
, то Х и Y являются зависимыми случайными величинами.
4. Если 
, то 
Из свойств коэффициента корреляции следует, что он является мерой тесноты линейной зависимости случайных величин Х и Y.
Если коэффициент корреляции двух случайных величин равен нулю, то эти величины называются некоррелированными.
| Для нормального распределения понятия независимости и некоррелируемости совпадают, т.е. если две нормальные величины не коррелированы, то они независимы |
В общем случае это утверждение неверно.
ПРИМЕР: Найти коэффициент корреляции величин Х и Y, совместный закон распределения которых задан таблицей:
| Y Х | 1 | 2 | 3 | 4 | å |
| 10 20 30 | 0,2 0,03 0,02 | 0,02 0,3 0,1 | 0,01 0,02 0,2 | 0 0 0,1 | 0,23 0,35 0,42 |
| å | 0,25 | 0,42 | 0,23 | 0,1 | 1,00 |
Используя приведенные выше формулы, последовательно найдем:
И окончательно найдем:
|
|
|
Рекомендуемая литература по теме 1.5: [1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 1.5:
1. Вероятность какого события задает сумма элементов первой строки матрицы распределения двумерной случайной величины?
2. Вероятность какого события задает сумма элементов первого столбца матрицы распределения двумерной случайной величины?
3. Чему равна сумма всех элементов матрицы распределения двумерной случайной величины?
____________________________________________________________
4. Какую величину определяет смешанная частная производная функции распределения двумерной случайной величины?
5. Чему равен коэффициент корреляции для двух независимых случайных величин?
____________________________________________________________
6. Чему равен коэффициент корреляции случайных величин Х и Y, если Y = 2X?
____________________________________________________________
Тема 1.6. Закон больших чисел
Неравенства Маркова и Чебышева
Если все значения случайной величины Х неотрицательны и существует ее математическое ожидание 
, то для любого числа e > 0 справедливо неравенство Маркова:
|
Если для случайной величины Х существует ее математическое ожидание и дисперсия 
, то для любого числа e > 0 справедливо неравенство Чебышева:
|
|
|
|
ПРИМЕР: Среднее число дождливых дней в году в данном районе равно 80. Оцените вероятность того, что в этом районе будет не более 100 дождливых дней в году.
Пусть случайная величина Х – число дождливых дней в году. Применив неравенство Маркова, получим:
Закон больших чисел
Приведем закон больших чисел (теорему Чебышева) в упрощенной формулировке, пригодной для решения практических задач.
Теорема Чебышева
Если случайные величины 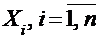 независимы и одинаково распределены с математическими ожиданиями  и дисперсиями, ограниченными постоянным числом С, т.е.  , то справедливо неравенство:
|
При n®¥ из неравенства теоремы Чебышева вытекает:
Закон больших чисел
|
Смысл закона больших чисел заключается в следующем. Хотя отдельные независимые случайные величины могут принимать значения далекие от своих математических ожиданий, среднее арифметическое достаточного большого числа случайных величин с большой, близкой к единице, вероятностью принимает значения весьма близкие к постоянному числу, равному математическому ожиданию этих величин.
|
|
|
Другими словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеяно мало.
ПРИМЕР: Номинальное значение диаметра втулки составляет 5 мм, а дисперсия, обусловленная погрешностью изготовления, не превосходит 0,01. Оцените вероятность того, что размер диаметра втулки будет отличаться от номинала не более, чем на 0,5 мм.
По теореме Чебышева: 
Теорема Бернулли
Частным случаем закона больших чисел является теорема Бернулли.
Теорема Бернулли
Пусть имеется n испытаний по схеме Бернулли с вероятностью успеха р и q = 1 – p и m – число успехов, тогда для любого
числа e > 0 справедливо неравенство:
|
Из неравенства теоремы Бернулли следует закон больших чисел в форме Бернулли:
|
Теорема Бернулли утверждает, что относительная частота события А стремится к его вероятности, так что при больших n отклонение относительной частоты от вероятности становится сколь угодно малым. Эту теорему в некотором смысле можно считать обоснованием статистического определения вероятности.
ПРИМЕР: Сколько следует провести независимых испытаний, чтобы вероятность выполнения неравенства 
превысила 0,75, если вероятность появления данного события в одном испытании составляет 0,8?
|
|
|
По теореме Бернулли запишем:
Дата добавления: 2018-06-01; просмотров: 1382; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!