Формула полной вероятности. Формулы Байеса

⇐ ПредыдущаяСтр 2 из 21Следующая ⇒

События 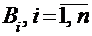образуют полную группу событий, если они попарно несовместны, а их сумма является достоверным событием, т.е.: B_i ∙ B_j = Ø при i ≠ j и 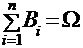. Такие события называются гипотезами.

По теореме сложения вероятностей для полной группы событий справедливо равенство: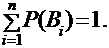

ПРИМЕР: В лесу растут деревья, среди которых 60% берез, 10% елей и 30% сосен. Для замеров деревьев случайным образом выбирается одно из них. Рассмотрим события: В₁ – «выбранное дерево береза», В₂ – «выбранное дерево ель», В₃ – «выбранное дерево сосна». Очевидно, что эти события попарно несовместны (если выбрали березу, то она не может оказаться ни елью, ни сосной), а сумма вероятностей этих событий равна 1. Значит, эти события образуют полную группу событий (являются гипотезами).

Пусть событие А может наступить только при осуществлении одного из событий 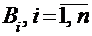, образующих полную группу. Тогда вероятность этого события определяется по формуле полной вероятности:

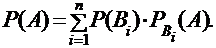
ПРИМЕР: Сохраним условия предыдущего примера. Пусть при замере диаметра деревьев он оказался больше 15 см для 30% берез, 40% елей и 70% сосен. Найдем вероятность события А – «диаметр случайно выбранного дерева больше 15 см». Условные вероятности события А равны: 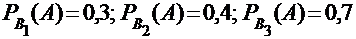. Тогда с учетом вероятностей гипотез из предыдущего примера по формуле полной вероятности найдем:

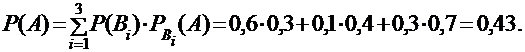
В формулу полной вероятности входят вероятности гипотез 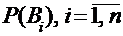, которые называются априорными. Если событие А уже наступило, то эти вероятности изменятся и будут условными вероятностями 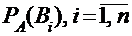, которые называются апостериорными. Эти вероятности могут быть найдены по формулам Байеса:

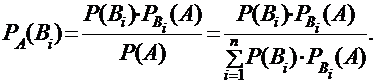
ПРИМЕР: Пусть в условиях предыдущего примера диаметр случайно выбранного дерева оказался больше 15 см, т.е. событие А наступило. Найти вероятность того, что измеренное дерево – береза.

По соответствующей формуле Байеса найдем:

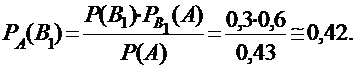
Рекомендуемая литература по теме 1.1:[1 ÷ 4].

ВОПРОСЫ для самопроверки знаний по теме 1.1:

1. В чем отличие между сочетанием из трех элементов по два и размещением из трех элементов по два?

2. Различаются ли понятия перестановки из трех элементов и размещения из трех элементов?

3. Может ли вероятность некоторого события быть равной 1,05?

4. Каким событием будет произведение несовместных событий?

5. Каким событием будет сумма события 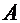и его дополнения ?

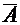6. Что больше: 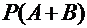или ?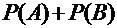

7. Чему равна сумма вероятностей всех событий, образующих полную группу?

____________________________________________________________

8. Могут ли изменяться вероятности гипотез после наступления события?

Тема 1.2. Повторение испытаний (схема Бернулли)

Формула Бернулли

Пусть производятся n независимых испытаний, в каждом из которых событие А может появиться или не появиться. Будем считать, что вероятность появления события А в каждом из этих испытаний одна и та же и равна p, а вероятность не появления события – равна: q = 1 – p, поскольку эти события противоположны. Появление события А будем называть «успехом», а не появление – «неуспехом». Такая схема называется последовательностью испытаний Бернулли или схемой Бернулли.

Пусть Х – число успехов в n испытаниях, тогда вероятность события (X = k) (ровно k успехов в n испытаниях) вычисляется по формуле Бернулли:

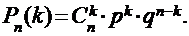
Эту формулу обычно используют при n < 15.

ПРИМЕР:Контрольный тест состоит из 4 вопросов. На каждый вопрос теста предлагается четыре варианта ответа, среди которых только один верный. Найти вероятность правильного ответа на все 4 вопроса теста для неподготовленного студента (выбирающего ответы наудачу).

Вероятность события А (правильный ответ) в каждом испытании (в каждом выборе ответа на вопрос теста) постоянна и равна р = 0,25, но тогда вероятность неправильного ответа: q = 1 – p = 0,75. Согласно условию задачи, n = k = 4, поэтому искомую вероятность найдем по формуле Бернулли:

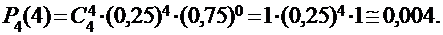
Формула Пуассона

Если в схеме Бернулли число испытаний n велико, вероятность р появления события А в каждом испытании мала, и произведение 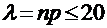, то вероятность того, что событие А появится ровно в k испытаниях можно найти по приближенной формуле Пуассона:

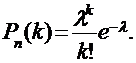
ПРИМЕР:В ходе проверки аудитор случайным образом отбирает 20 счетов. Найти вероятность того, что он обнаружит 2 счета с ошибкой, если в среднем 3% счетов содержат ошибки.

По условию задачи: n = 20, p = 0,03, λ = n∙p = 0,6. Применяя формулу Пуассона, получим:

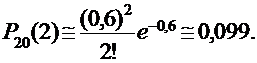
Локальная формула Лапласа

При больших n вероятность появления события А ровно k раз в схеме из n испытаний Бернулли можно вычислять по локальной формуле Лапласа:

,

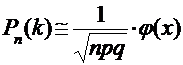где: 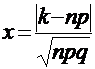, а функция 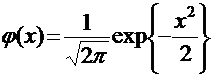есть малая функция Лапласа, значения которой имеются в соответствующих таблицах.

ПРИМЕР: Вероятность найти белый гриб среди прочих равна 0,25. Какова вероятность того, что среди 80 найденных грибов белых будет ровно 20?

По условию задачи n = 80, k = 20, p = 0,25, q = 0,75, поэтому, вычислим:

.

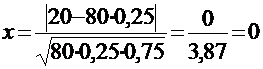По таблице, например, приложения 2 к учебному пособию [2] найдем 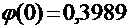и окончательно по локальной формуле Лапласа найдем:

Интегральная формула Лапласа

Вероятность того, что число k появления события А в схеме Бернулли находится в заданном промежутке: 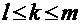, при большом числе испытаний n определяется по интегральной формуле Лапласа:

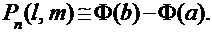
В этой формуле приняты следующие обозначения:

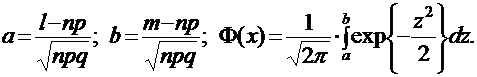
Функцию Φ(х) называют интегральной функцией Лапласа, а ее значения можно найти в соответствующих таблицах.

При вычислениях по интегральной формуле Лапласа следует иметь в виду, что интегральная функция Лапласа является нечетной функцией, т.е. .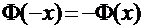

ПРИМЕР: Вероятность выпуска цехом завода бракованных деталей постоянна и равна 0,1. Найти вероятность того, что среди изготовленных цехом 100 деталей будет не менее 85 стандартных.

По условию задачи: n = 100, р = 0,9, q = 0,1, l = 85, m = 100. Найдем аргументы функции Лапласа:

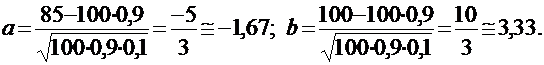
По таблице, например, приложения 3 к пособию [2], найдем для этих значений аргумента значения интегральной функции Лапласа:

,

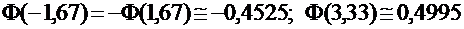и окончательно получим:

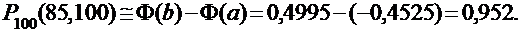
Для относительной частоты m / n появления события А в n испытаниях по схеме Бернулли справедлива приближенная формула:

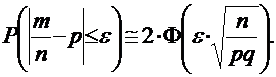
ПРИМЕР: Сколько нужно произвести бросаний монеты, чтобы с вероятностью 0,95 можно было утверждать, что относительная частота выпадения герба отличается от вероятности 0,5 по модулю не более чем на .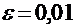

С использованием приведенной формулы можно записать:

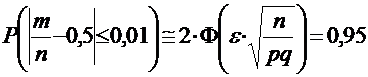,откуда получим:

.

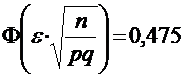По таблицам значений функции Лапласа найдем: 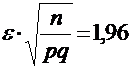. Но тогда: .

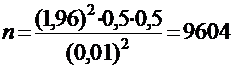Рекомендуемая литература по теме 1.2:[1 ÷ 4].

ВОПРОСЫ для самопроверки знаний по теме 1.2:

1. Можно ли считать схемой Бернулли многократное бросание игральной кости?

____________________________________________________________

2. Может ли в схеме Бернулли при n = 10 и р = 0,1 наивероятнейшее число успехов быть больше 2?

3. Как находится параметр х в локальной формуле Лапласа?

4. Какая функция используется для оценки вероятности в интегральной формуле Лапласа?

5. По какой формуле оценивается вероятность заданного отклонения относительной частоты от вероятности в схеме Бернулли?

6. В каких случаях более предпочтительно применение локальной формулы Лапласа, а не формулы Бернулли?

____________________________________________________________

Тема 1.3. Случайные величины

Случайной величиной называется величина, которая в результате одного испытания принимает одно и только одно возможное значение, априори неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

ПРИМЕРЫ:

1. Количество родившихся мальчиков среди 100 новорожденных есть случайная величина, а числа от 0 до 100 – возможные значения этой случайной величины.

2. Расстояние, которое пролетает снаряд при выстреле из орудия, есть случайная величина, возможные значения которой располагаются в пределах отрезка с границами, соответствующими минимальной и максимальной дальности полета снаряда.

Случайные величины принято обозначать прописными латинскими буквами: X, Y, Z и т.д., а их возможные значения – строчными буквами: x, y, z и т.д.

Функцией распределения случайной величины Х называется функция F(x), определяющая вероятность того, что величина Х примет значение, меньшее х, т.е. F(x) = P(X < x).

Дата добавления: 2018-06-01; просмотров: 762; Мы поможем в написании вашей работы!
Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!