Показательное (экспоненциальное) распределение
Непрерывная случайная величина Х имеет показательное (экспоненциальное) распределение с параметром l > 0, если ее плотность распределения имеет вид:
|
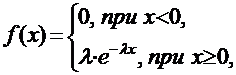
Функция распределения случайной величины, распределенной по показательному закону, имеет вид:
|
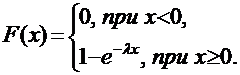
Графики плотности распределения и функции распределения показательного распределения приведены на рис. 1.3 и 1.4 соответственно.
Математическое ожидание и дисперсия показательно распределенной случайной величины Х определяется формулами
|
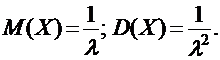
ПРИМЕР: Установлено, что время Т горения электрической лампочки является случайной величиной, распределенной по показательному закону. Считая, что среднее значение этой величины равно 6 месяцам, найти вероятность того, что лампочка будет гореть в течение года.
Т.к.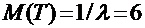 
, то l = 1 / 6, а функция распределения случайной величины Т будет иметь вид:
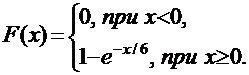
Поэтому можно найти:
Нормальное распределение
Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами а и s > 0, если ее плотность распределения имеет вид:
|
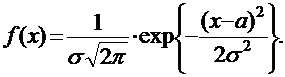
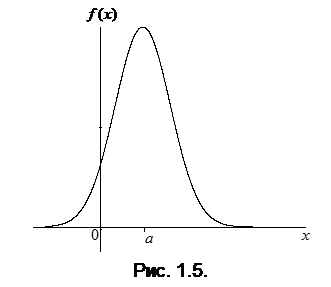
График плотности вероятности нормально распределенной случайной величины приведен на рис. 1.5.
 |
Функция распределения нормально распределенной случайной величины имеет вид:
|
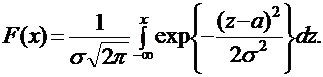
Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а, а дисперсия равна квадрату параметра s, т.е.
|
|
|
|
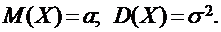
При а = 0 и s = 1 нормальное распределение называется стандартным нормальным или нормированным нормальным распределением.
Для стандартного нормального распределения плотность вероятности будет иметь вид:
,
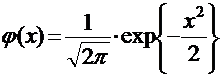а введенная ранее интегральная функция Лапласа:
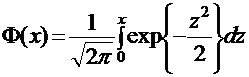
задает вероятность попадания значения нормально распределенной величины Х в интервал (0, х). Очевидно, что вероятность попадания значения нормально распределенной случайной величины с параметрами а и s в интервал (a, b) определяется формулой:
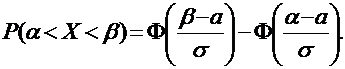
ПРИМЕР: Текущая цена ценной бумаги является нормально распределенной случайной величиной Х с математическим ожиданием 100 у.е. и дисперсией 9 (у.е.)2. Найти вероятность того, что цена актива будет находиться в пределах от 91 до 109 у.е.
Поскольку а = 100, 
, a = 91 и b = 109, для искомой вероятности можно записать:
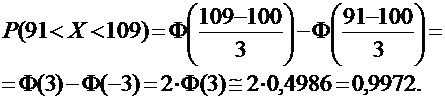
Рекомендуемая литература по теме 1.4: [1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 1.4:
1. Какие значения может принимать биномиально распределенная случайная величина?
2. Какими параметрами определяется биномиальное распределение?
|
|
|
____________________________________________________________
3. Какими параметрами определяется геометрическое распределение?
____________________________________________________________
4. Какие значения может принимать случайная величина, имеющая распределение Пуассона?
5. Какой смысл имеет параметр l в пуассоновском распределении?
6. Чему равны математическое ожидание и дисперсия равномерно распределенной случайной величины?
7. Может ли случайная величина, распределенная по показательному закону, принимать отрицательные значения?
____________________________________________________________
8. Как влияют параметры а и s нормального распределения на форму графика его плотности распределения?
Тема 1.5. Система двух случайных величин
Набор n случайных величин {X1, X2, …, Xn} называется многомерной случайной величиной.
Многомерная случайная величина каждому элементарному событию ставит в соответствие n действительных чисел (х1, х2, …, хn), которые являются значениями, принятыми случайными величинами Х1, Х2, …, Xn в результате испытания.
В частности, набор двух случайных величин (X, Y) называется двумерной случайной величиной, при этом каждая из случайных величин Х и Y называется компонентой двумерной случайной величины. Обе случайные величины Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
|
|
|
ПРИМЕР: Цена С единицы товара и количество V товара на рынке представляют собой двумерную случайную величину.
Дата добавления: 2018-06-01; просмотров: 441; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!