Дискретные двумерные случайные величины
Если случайные величины Х и Y дискретны, то двумерная случайная величина (Х, Y) называется дискретной. Дискретная двумерная случайная величина может принимать конечное или счетное множество значений, каждое из которых представляет собой пару действительных чисел (х, y).
Законом распределения дискретной двумерной случайной величины называется множество ее значений и вероятностей этих значений:
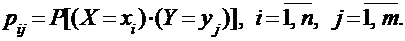
Закон распределения двумерной дискретной случайной величины с конечным числом значений можно представить в виде матрицы размером n x m, каждым элементом которой будут вероятности 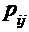 .
.
Пусть 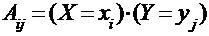 есть событие, состоящее в том, что случайная величина Х примет значение xi , а случайная величина Y примет значение yj . Тогда очевидно, что любые два таких события будут несовместны, а все они в совокупности образуют полную группу событий. Поэтому справедливо равенство:
есть событие, состоящее в том, что случайная величина Х примет значение xi , а случайная величина Y примет значение yj . Тогда очевидно, что любые два таких события будут несовместны, а все они в совокупности образуют полную группу событий. Поэтому справедливо равенство:
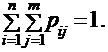
Распределения одномерных случайных величин Х и Y, составляющих двумерную случайную величину (Х, Y), определяются формулами:
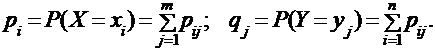
Таким образом, суммируя элементы матрицы вероятностей по строкам, получим распределение случайной величины Х, а по столбцам – величины Y.
Если считать, что событие  произошло, то распределение случайной величины Х называется условным распределением. Из определения условной вероятности найдем:
произошло, то распределение случайной величины Х называется условным распределением. Из определения условной вероятности найдем:
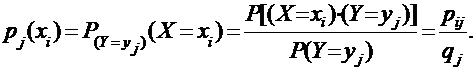
Аналогично условное распределение случайной величины Y при условии 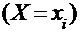 задается формулой:
задается формулой:
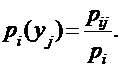
Функция распределения двумерной случайной величины
Функцией распределения двумерной случайной величины 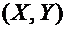 называется функция
называется функция  , определяющая для каждой пары чисел
, определяющая для каждой пары чисел 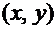 вероятность того, что величина Х примет значение, меньшее х, и при этом величина Y примет значение, меньшее y, т.е.
вероятность того, что величина Х примет значение, меньшее х, и при этом величина Y примет значение, меньшее y, т.е.
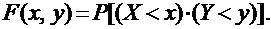
Для дискретной двумерной случайной величины функция распределения определяется формулой:
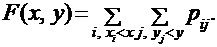
Основные свойства функции распределения:
1. 
2. Функция распределения есть неубывающая функция по каждому из аргументов, т.е. 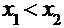 Þ
Þ 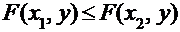 и
и 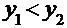 Þ
Þ 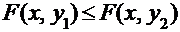 .
.
3. 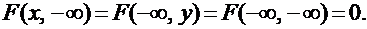
4. 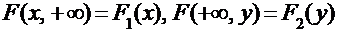 , где:
, где: 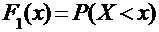 и
и 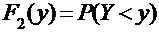 являются функциями распределения случайных величин
являются функциями распределения случайных величин 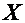 и
и 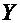 .
.
5. 
Непрерывные двумерные случайные величины
Непрерывной называется двумерная случайная величина 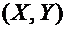 , если ее функция распределения
, если ее функция распределения  непрерывна по обоим аргументам.
непрерывна по обоим аргументам.
Для непрерывной двумерной случайной величины функцию распределения можно записать в виде:
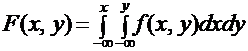 ,
,
где функция  называется плотностью распределения двумерной случайной величины, или совместной плотностью вероятностей случайных величин
называется плотностью распределения двумерной случайной величины, или совместной плотностью вероятностей случайных величин 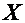 и
и 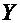 . Плотность распределения связана с функцией распределения формулой:
. Плотность распределения связана с функцией распределения формулой:
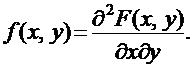
Свойства плотности распределения:
1. 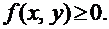
2. 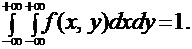
Если S – некоторая область в двумерном пространстве, то вероятность попадания двумерной случайной величины в эту область выражается формулой:
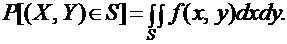
В частности, если область S представляет собой прямоугольник с вершинами 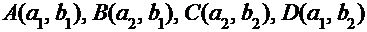 (рис. 1.6), то вероятность попадания случайной величины в этот прямоугольник будет равна:
(рис. 1.6), то вероятность попадания случайной величины в этот прямоугольник будет равна:
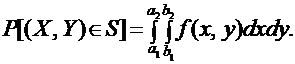
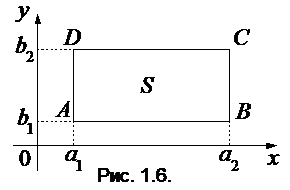 |
С помощью известной совместной плотности двух случайных величин Х и Y можно найти одномерные плотности распределения  и
и  этих величин по формулам:
этих величин по формулам:
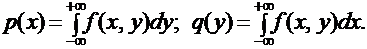
Дата добавления: 2018-06-01; просмотров: 460; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
