Дискретные случайные величины
Дискретной называется случайная величина, которая принимает отдельные, изолированные друг от друга возможные значения, или множество ее возможных значений является конечным или счетным.
3. ПРИМЕР:В предыдущем примере количество родившихся мальчиков среди 100 новорожденных есть дискретная случайная величина, а числа от 0 до 100 – возможные значения этой дискретной случайной величины.
Законом распределения дискретной случайной величины Х называется соответствие между ее возможными значениями и их вероятностями, т.е. вероятностями событий (Х = х). При этом закон распределения может быть задан таблично (в виде таблицы), аналитически (в виде формулы для расчета вероятностей) и графически (в виде полигона).
Наиболее часто закон распределения дискретной случайной величины задается в виде таблицы:
| Х | х1 | х2 | … | хn |
| Р | р1 | р2 | … | рn |
Поскольку в одном испытании случайная величина может принять одно и только одно возможное значение, события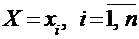 
образуют полную группу, поэтому: 
.
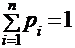ПРИМЕР: В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 1000 рублей и 10 выигрышей по 100 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша владельца одного лотерейного билета.
Возможными значениями величины Х являются: х1 = 1000, х2 = 100, х3 = 0. Вероятности этих возможных значений таковы: р1 = 0,01; р2 = 0,1 и р3 = 1 – (р1 + р2) = 0,89. Поэтому искомый закон распределения можно представить в виде:
|
|
|
| Х | 1000 | 100 | 0 |
| Р | 0,01 | 0,1 | 0,89 |
Кроме закона распределения, дискретную случайную можно характеризовать числовыми характеристиками: математическим ожиданием и дисперсией.
Математическим ожиданием М(Х)дискретной случайной величины Х называется число, определяемой формулой:
|
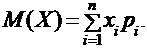
Математическое ожидание имеет смысл среднего значения случайной величины. Если число возможных значений случайной величины Х конечно и равно n, а вероятности этих значений pn = 1 / n, то математическое ожидание совпадает с обычным средним значением величин 
, т.е.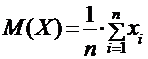 
.
Математическое ожидание обладает следующими основными свойствами:
1. М(С) = С, где С – постоянная величина.
2. М(СХ) = С×М(Х), где С – постоянная величина.
3. М(Х ± Y) = M(X) ± M(Y) для любых величин Х и Y.
4. M(X×Y) = M(X)×M(Y), если Х и Y – независимые величины.
Для оценки степени рассеивания значений случайной величины вокруг ее среднего значения вводится понятие дисперсии.
Дисперсией D(X) случайной величины Х называется число, равное математическому ожиданию квадрата разности [X – M(X)], для дискретных случайных величин дисперсия определяется формулой:
|
|
|
|
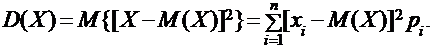
Для практических вычислений дисперсии обычно используют более удобную формулу:
|
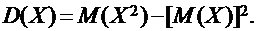
Дисперсия обладает следующими основными свойствами:
1. D(C) = 0, где С – постоянная величина.
2. D(CX) = C2D(X), где С – постоянная величина.
3. D(X ± Y) = D(X) + D(Y), если Х и Y – независимые величины.
Другой мерой рассеивания случайной величины, имеющей ту же размерность, что и сама случайная величина, является среднее квадратическое отклонение.
Средним квадратическим отклонением s(Х) случайной величины Х называется число, определяемое формулой:
 .
|
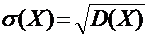ПРИМЕР:Для дискретной случайной величины Х – стоимости выигрыша владельца одного лотерейного билета предыдущего примера имеем:
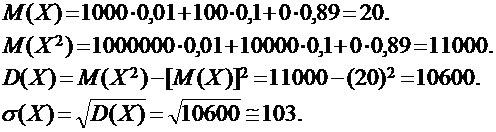
Для дискретной случайной величины с известным законом распределения функция распределения будет являться кусочно-постоянной функцией с ординатами:
|
При этом скачки значений функции F(x) в точках разрыва x = xi будут равны pi.
ПРИМЕР: Для дискретной случайной величины Х, заданной законом распределения:
| Х | 1 | 2 | 3 | 4 |
| Р | 0,3 | 0,2 | 0,1 | 0,4 |
 |
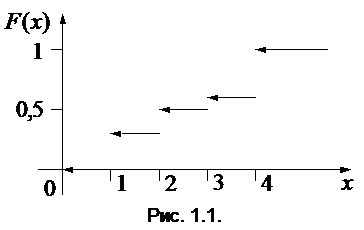график функции распределения будет иметь вид, представленный на рис. 1.1.
|
|
|
Перечислим основные свойства функции распределения:
1. Функция распределения – монотонно неубывающая функция.
2. Функция распределения непрерывна слева.
3. 
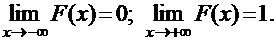
Дата добавления: 2018-06-01; просмотров: 323; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!