Понятие о центральной предельной теореме

⇐ ПредыдущаяСтр 8 из 21Следующая ⇒

На практике выясняется, что многие случайные величины имеют нормальное распределение. Это обстоятельство во многом определяется тем, что каждую такую величину можно рассматривать как сумму большого числа случайных величин, имеющих самые разнообразные законы распределения, а такое суммирование приводит в итоге к нормальному распределению этой суммы.

Это свойство устанавливается доказанной русским математиком Ляпуновым центральной предельной теоремой.

Центральная предельная теорема

Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то величина Х имеет распределение вероятностей, весьма близкое к нормальному распределению.

ПРИМЕР: Пусть случайная величина Х – потребление электроэнергии в год в некотором городе. Очевидно, что суммарное потребление складывается из потребления электроэнергии отдельными потребителями, каждое из которых принимает случайные значения с разными законами распределения. Центральная предельная теорема утверждает, что и в этом случае, какое бы распределение не имели отдельные составляющие общегородского потребления, распределение этого общего, суммарного потребления (величины Х) будет близко к нормальному распределению.

Рекомендуемая литература по теме 1.6:[1 ÷ 4].

ВОПРОСЫ для самопроверки знаний по теме 1.6:

1. Какие значения может принимать случайная величина, для которой выполняется неравенство Маркова?

2. При каком условии справедливо неравенство Чебышева?

3. К чему стремится среднее значение случайных величин согласно закону больших чисел?

4. К чему стремится относительная частота события при неограниченном увеличении числа испытаний в схеме Бернулли?

5. Какое основное условие налагает центральная предельная теорема на составляющие суммарной случайной величины?

ТЕМА 1.7. Цепи Маркова

Понятие марковского случайного процесса

Пусть имеется некоторая физическая система S, состояние которой может меняться с течением времени. Заметим, что под такой системой можно понимать: любое техническое устройство, ремонтную мастерскую, компьютер, железнодорожный узел и т.п. Если состояние такой системы меняется во времени случайным, заранее непредсказуемым образом, то говорят: в данной системе протекает случайный процесс. Например, процесс функционирования компьютера, процесс обслуживания клиентов в ремонтной мастерской и т.п.

Случайный процесс, протекающий в системе S, называется марковским процессом, или процессом без последействия, если для каждого момента времени t₀ вероятность любого состояния системы в будущем (при t > t₀) зависит только от ее состояния в настоящем (при t = t₀) и не зависит от того, когда и каким образом система пришла в это состояние.

Таким образом, в марковском случайном процессе будущее его протекание зависит только от настоящего его состояния и не зависит от «предыстории» процесса.

Марковский случайный процесс называется процессом с дискретными состояниями, если возможные состояния системы можно перечислить, или пронумеровать, а сам этот процесс состоит в том, что время от времени система скачком (мгновенно) перескакивает из одного состояние в другое.

ПРИМЕР:Пусть некоторое техническое устройство состоит из двух узлов, каждый из которых в процессе работы устройства может отказать. Возможные состояния системы: S₁ – оба узла работают; S₂ – первый узел отказал, а второй работает; S₃ – отказал второй узел, а первый работает; S₄ – оба узла отказали. Можно считать, что в данной системе протекает марковский случайный процесс с дискретными состояниями, а переход системы из одного состояние в другое происходит мгновенно по мере отказа узлов устройства.

При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой – графом состояний, на котором квадратами изображают возможные состояния системы, а возможные переходы системы – стрелками, соединяющими эти квадраты. На рис. 1.7. представлен граф состояний системы предыдущего примера.

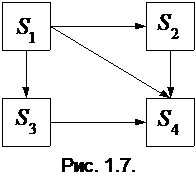Дата добавления: 2018-06-01; просмотров: 389; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!