Цепи Маркова с непрерывным временем
Марковский случайный процесс называется процессом с непрерывным временем, если переходы системы из состояния в состояние возможны в любой, заранее неизвестный, случайный момент времени. Модель такого процесса называют цепью Маркова с непрерывным временем.
В случае непрерывной цепи Маркова для отыскания вероятностей состояний системы в любой момент времени t, т.е. функций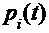 
, вместо вероятностей перехода используют плотности вероятностей перехода системы 
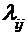из состояния 
в состояние 
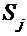, которые определены только когда 
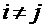. Эти плотности вероятностей указывают на размеченном графе состояний системы над стрелками возможных переходов.
Используя размеченный граф состояний, составляется система дифференциальных уравнений Колмогорова, решениями которой и являются функции вероятностей состояний от времени. При составлении системы таких уравнений полезно пользоваться следующими правилами:
Правила составления системы дифференциальных уравнений Колмогорова
1. Левая часть каждого уравнения содержит производную вероятности того состояния, для которого записывается уравнение.
2. Правая часть каждого уравнения содержит столько слагаемых, сколько стрелок связано с данным состоянием.
3. Если стрелка исходит из состояния, то соответствующее этой стрелке слагаемое в правой части имеет знак “минус”, если же стрелка входит в данное состояние, то – знак “плюс”.
|
|
|
4. Каждое слагаемое правой части уравнения есть произведение плотности вероятности перехода, соответствующей данной стрелке, на вероятность того состояния, из которого исходит данная стрелка.
Алгоритм решения системы дифференциальных уравнений Колмогорова можно найти в пособии [5].
 |
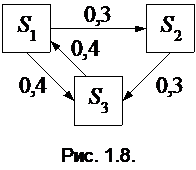ПРИМЕР:В некоторой системе с тремя состояниями протекает марковский случайный процесс с непрерывным временем. Составьте систему дифференциальных уравнений Колмогорова, используя размеченный граф состояний системы, представленный на рис. 1.8.
Используя размеченный граф состояний системы и правила, перечисленные выше, найдем:
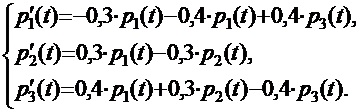
или, окончательно:
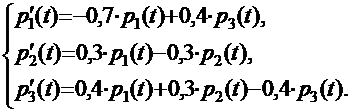
Рекомендуемая литература по теме 1.7:[1 ÷ 4, 5].
ВОПРОСЫ для самопроверки знаний по теме 1.7:
1. Что отличает марковский случайный процесс с дискретными состояниями от других случайных процессов?
____________________________________________________________
____________________________________________________________
2. В какие моменты времени могут происходить переходы системы из состояния в состояние для цепи Маркова с дискретным временем?
3. Какие вероятности можно найти, используя равенство Маркова?
|
|
|
4. В какие моменты времени могут происходить переходы системы из состояния в состояние для цепи Маркова с непрерывным временем?
5. С помощью чего отыскиваются вероятности состояний для цепи Маркова с непрерывным временем?
РАЗДЕЛ 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Предметом математической статистики является изучение случайных событий и случайных величин по результатам наблюдений. Статистической совокупностью называется совокупность предметов или явлений, объединенных каким-либо признаком. Результатом наблюдений над статистической совокупностью являются статистические данные – сведения о том, какие значения принял в итоге наблюдений интересующий нас признак.
Обработка статистических данных методами математической статистики приводит к установлению определенных закономерностей, присущих массовым явлениям. При этом достоверность статистических выводов повышается с ростом числа наблюдений.
Статистические данные, как правило, представляют собой некоторый ряд значений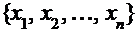 
случайной величины Х. Исследование случайной величины начинается с обработки этого ряда значений. Затем строятся функции, характеризующие эту случайную величину, и называемые статистиками.
|
|
|
Следовательно, статистика – это функция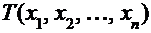 
, которая каждому набору значений 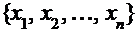случайной величины поставляет по некоторому правилу действительное число.
В теоретических исследованиях удобно рассматривать статистику Т как функцию от случайных величин 
, имеющих такое же распределение, как и случайная величина Х, т.е.: 
.
Таким образом, всякую случайную величину Х можно рассматривать как набор одинаково распределенных случайных величин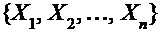 
. В такой трактовке статистика становится случайной величиной, а изучение ее распределения приводит к выводам о распределении случайной величины Х.
ПРИМЕР: Пусть Х – нормально распределенная случайная величина и имеется n ее наблюдений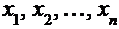 
. Простейшей статистикой этой случайной величины является ее среднее значение: 
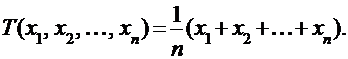Тогда вместе со случайной величиной Х возникает набор случайных величин 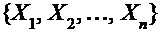и новая случайная величина: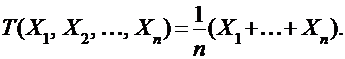 
Дата добавления: 2018-06-01; просмотров: 638; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!