Основные законы распределения статистических оценок
Распределение статистических оценок в большинстве случаев достаточно точно описывается такими законами распределения, как: нормальный, «хи-квадрат», Стьюдента и Фишера-Снедекора. Поскольку нормальное распределение было достаточно подробно рассмотрено выше, рассмотрим другие распределения.
Распределение «хи-квадрат»
Пусть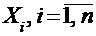 
независимые нормально распределенные случайные величины с нулевым математическим ожиданием и средним квадратическим отклонением, равным единице. Тогда закон распределения суммы квадратов этих случайных величин, т.е. случайной величины: 
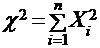, называется законом «хи-квадрат» с n степенями свободы. Если же эти величины связаны одним линейным соотношением, например, 
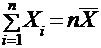, то число степеней свободы уменьшается на единицу и становится равным 
.
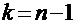Распределение «хи-квадрат» определяется только одним параметром – числом степеней свободы k. С увеличением числа степеней свободы это распределение медленно приближается к нормальному распределению.
Распределение Стьюдента
Пусть 
совокупность независимых нормально распределенных случайных величин, имеющих нулевые математические ожидания и средние квадратические отклонения, равные единице. Тогда случайная величина:
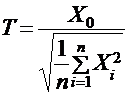
имеет распределение Стьюдента, или T-распределение, с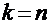 
степенями свободы (Стьюдент – псевдоним английского статистика В. Госсета).
|
|
|
Для решения практических задач часто используется случайная величина, определяемая формулой:
,
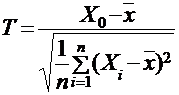также имеющая распределение Стьюдента, но уже с 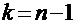степенями свободы.
Это распределение определяется только одним параметром – числом степеней свободы k. С возрастанием числа степеней свободы распределение Стьюдента довольно быстро приближается к нормальному распределению.
Распределение Фишера-Снедекора
Пусть 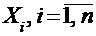и 
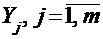совокупности независимых нормально распределенных случайных величин, имеющих нулевые математические ожидания и средние квадратические отклонения, равные единице. Тогда случайная величина:
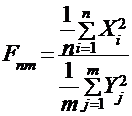
имеет распределение Фишера-Снедекора с n и m степенями свободы.
Распределение Фишера-Снедекора определяется только двумя параметрами – числами степеней свободы n и m.
Если случайные величины X и Y связаны, например, с помощью выборочных средних, то случайная величина:
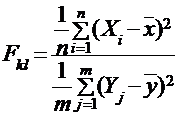
также имеет распределение Фишера-Снедекора с числами степеней свободы 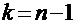и 
, соответственно.
Интервальные оценки параметров
Точечная оценка параметра дает лишь некоторое приближенное значение его. Чтобы получить представление о точности и надежности оценки, используют интервальную оценку параметра.
|
|
|
Интервальной оценкой параметра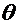 
называется интервал 
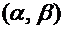, который с заданной вероятностью 
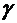накрывает неизвестное значение параметра 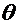. При этом интервал 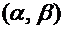называется доверительным интервалом, а вероятность 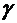называется доверительной вероятностью или уровнем надежности. Доверительная вероятность обычно задается числом, близким к единице: 0,95; 0,99 или 0,999.
Обычно доверительный интервал имеет вид 
и определяется формулой:
,
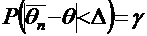где отклонение выборочного значения параметра от его истинного значения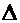 
называется предельной ошибкой выборки.
Пусть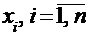 
выборка из генеральной совокупности объема 
, 
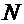выборочная средняя, 
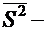исправленная выборочная дисперсия, 
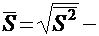выборочное среднее квадратическое отклонение и 
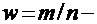выборочная доля признака.
Доверительный интервал уровня надежности 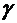для генеральной средней 
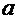имеет вид: 
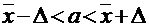, где Δ – предельная ошибка выборки, зависящая от .
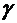При n > 30 для повторной выборки:
,
а для бесповторной выборки:
.
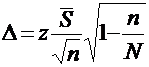Причем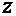 
определяется из условия: 
, где 
интегральная функция Лапласа.
Если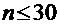 
(выборка малого объема), то доверительный интервал для генеральной средней строится только для нормальной генеральной совокупности. При этом для повторной выборки:
|
|
|
,
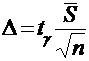а для бесповторной выборки:
,
где значение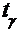 
находится по таблицам распределения Стьюдента по заданным значениям 
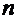и .
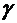Доверительный интервал для генеральной доли р имеет вид: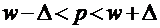 
, где при 
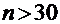для повторной выборки:
,
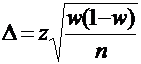а для бесповторной выборки:
,
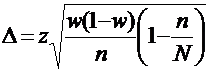где 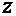определяется условием .
При 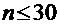рассматриваются только выборки из нормальной генеральной совокупности, а предельные ошибки выборки определяются по тем же формулам.
ПРИМЕРЫ:
1. Из партии в 5000 электрических ламп отобрано 300 по схеме бесповторной выборки. Средняя продолжительность горения ламп в выборке оказалась равной 1450 часам, а дисперсия – 4000. Найти доверительный интервал для среднего срока горения лампы с надежностью 0,9996.
Для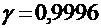 
по таблицам находим 
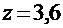. При 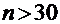для бесповторной выборки найдем:
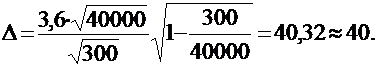
Следовательно, искомый доверительный интервал: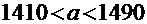 
.
2. В партии, содержащей 5000 изделий, проверено 400. Среди них оказалось 300 изделий высшего сорта. Найти с надежностью 0,95 доверительный интервал для доли изделий высшего сорта в случаях повторной и бесповторной выборок.
Для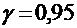 
по таблицам находим 
. При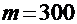 
, 
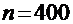найдем выборочную долю 
. Для случая повторной выборки предельная ошибка будет равна:
|
|
|
,
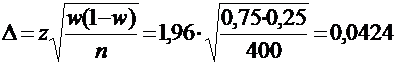а доверительный интервал будет иметь вид: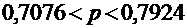 
.
Для бесповторной выборки:
,
а доверительный интервал: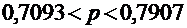 
.
Рекомендуемая литература по теме 2.2:[1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 2.2:
1. Будет ли выборочная средняя несмещенной и состоятельной оценкой для математического ожидания?
____________________________________________________________
2. Какая из оценок дисперсии: выборочная или исправленная выборочная является несмещенной для генеральной дисперсии?
3. Какими свойствами обладает выборочная доля в качестве оценки генеральной доли?
4. Какая связь между доверительным интервалом и истинным значением оцениваемого параметра?
5. Как предельная ошибка выборки связана с доверительным интервалом?
6. Как отличаются предельные ошибки для повторной и бесповторной выборок при интервальной оценке генеральной средней?
Дата добавления: 2018-06-01; просмотров: 418; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!