Проверка гипотезы о распределении генеральной совокупности. Критерии согласия

Рассмотрим наиболее часто применяемый в статистической практике критерий согласия Пирсона.

Пусть выборка из генеральной совокупности Х, а предполагаемая функция теоретического распределения. Пусть также по данным выборки построен интервальный вариацион­ный ряд , где число элементов выборки, попавших в интервал . Для каждого интервала  вычислим теоретические вероятности 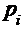 попадания случайной величины Х в этот интервал:

.

Числа 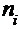 и  называются эмпирическими и теоретиче­скими частотами. Доказано, что при  статистика:

имеет распределение  (хи – квадрат) с  степенями свободы, где число интервалов вариационного ряда, а число параметров, которыми определяется теоретическое распределение.

Нулевая гипотеза в данном случае состоит в том, что функцией распределения случайной величины Х (в генеральной совокупности) является выбранная теоретическая функция.

Для заданного уровня значимости  и найденного количества степеней свободы  по таблицам критических точек распределения  находим значение , а по приведенной выше формуле находим наблюдаемое значение критерия .

Нулевая гипотеза принимается, если , В противном случае говорят, что данные наблюдений дают основание отвергнуть нулевую гипотезу.

Заметим, что критерий Пирсона следует применять только при достаточно больших объемах выборки: .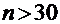

ПРИМЕР: Пользуясь критерием Пирсона, при  прове­рить нулевую гипотезу о нормальности распределения генеральной совокупности, если по выборке объемом 50 получен интервальный вариационный ряд представленный в таблице:

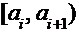
	[-2,0; -1,2)	[-1,2; -0,4)	[-0,4; 0,4)	[0,4; 1,2)	[1,2; 2,0)
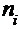
	6	11	21	7	5

Построим гистограмму выборочного распределения (рис. 2.7). По ее виду можно предположить, что случайная величина распределена по нормальному закону.

Вычислим выборочные среднюю и дисперсию:

.

Затем найдем теоретические частоты попадания в интервалы по формуле:

.

Для удобства вычислений составим таблицу, где: .

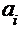
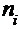
1 2 3 4 5 6	-2,0 -1,2 -0,4 0,4 1,2 2,0	-2,13 -1,23 -0,34 0,55 1,45 2,34	-0,4834 -0,3907 -0,1331 0,2088 0,4265 0,4904	[-2; -1,2) [-1,2; -0,4) [-0,4; 0,4) [0,4; 1,2) [1,2; 2,0)	6 11 21 7 5	4,64 12,88 17,10 10,88 3,20	0,399 0,274 0,889 1,384 1,012
					50	48,7	3,958

В последней строке последнего столбца таблицы располагается наблюдаемое значение критерия Пирсона . По таблице критических точек для уровня значимости  и числа степеней свободы  находим критическую точку . Поскольку , данные наблюдений не дают оснований отверг­нуть нулевую гипотезу. Следовательно, с уровнем доверия 0,95 можно считать, что генеральная совокупность имеет нормальное распреде­ление.

Рекомендуемая литература по теме 2.3:[1 ÷ 4].

ВОПРОСЫ для самопроверки знаний по теме 2.3:

1. Как связаны вероятность ошибки первого рода и уровень доверия?

____________________________________________________________

2. Как связаны вероятность ошибки второго рода и мощность критерия?

____________________________________________________________

3. В какие области попадает наблюдаемое значение критерия при принятии и непринятии нулевой гипотезы?

4. Какого вида бывают критические области?

5. Какой критерий используется для проверки гипотезы о равенстве генеральных средних?

____________________________________________________________

6. Какой критерий используется для проверки гипотезы о равенстве генеральных дисперсий?

____________________________________________________________

7. Какой критерий используется для проверки гипотезы о законе распределения генеральной совокупности?

____________________________________________________________

Мы поможем в написании ваших работ!