Выборочный коэффициент корреляции
Основной оценкой для тесноты связи между переменными величинами Х и Y служит выборочный коэффициент корреляции, который определяется формулой:
 .
|
Свойства выборочного коэффициента корреляции аналогичны свойствам коэффициента корреляции случайных величин Х и Y.
Свойства выборочного коэффициента корреляции
1. Выборочный коэффициент корреляции может принимать значения на отрезке 
, т.е. 
. При этом в зависимости от значений 
различают слабую, умеренную и сильную связь, т.е. чем ближе к единице, тем теснее связь.
2. Если 
, то корреляционная связь между Х и Y представляет собой функциональную линейную зависимость.
Запишем более подробные формулы для вычисления коэффициента корреляции для случая сгруппированных (представленных в виде корреляционной таблицы) данных.
,
Если данные не сгруппированы, то приведенные формулы значительно упрощаются:
,
Поскольку значение 
вычисляется по данным выборки, то, в отличие от генерального коэффициента корреляции ρ, является величиной случайной. Если получено 
, то возникает вопрос, объясняется ли это действительно существующей корреляционной связью между Х и Y или вызвано случайными факторами. Для выяснения значимости коэффициента корреляции проверяется нулевая гипотеза об отсутствии корреляционной связи между изучаемыми признаками, т.е. 
. При справедливости этой гипотезы статистика:
|
|
|
имеет распределение Стьюдента с 
степенями свободы. Поэтому нулевая гипотеза отвергается, если 
, где значение 
находится по таблицам критических точек распределения Стьюдента для уровня значимости α и числа степеней свободы .
ПРИМЕР:По данным таблицы 2.1 предыдущего подраздела найти выборочный коэффициент корреляции и проверить его значимость на уровне 
.
Для вычисления всех сумм, входящих в формулу выборочного коэффициента корреляции в случае сгруппированных данных, составим и заполним вспомогательную вычислительную таблицу.
| 
| 
| 
| 
| 
| 
| 
| 
|
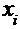
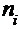
| 1 | 12,5 | 1 | 20,5 | 1 | 12,5 | 20,5 | 156,25 | 420,25 |
| 2 | 17,5 | 3 | 21,5 | 2 | 52,5 | 43,0 | 918,75 | 924,5 |
| 3 | 22,5 | 5 | 22,5 | 3 | 112,5 | 67,5 | 2531,25 | 1518,75 |
| 4 | 27,5 | 11 | 23,5 | 6 | 302,5 | 141,0 | 8318,75 | 3313,5 |
| 5 | - | - | 24,5 | 8 | - | 196,0 | - | 4802,0 |
| - | - | - | - | 480,0 | 468,0 | 11925,0 | 10979,0 |
Таким образом, найдены следующие суммы:
.
Найдем еще одну сумму:
Подставляя полученные значения сумм в соответствующую формулу, найдем значение выборочного коэффициента корреляции:
Проверим значимость на уровне , для чего вычислим наблюдаемое значение критерия Стьюдента:
|
|
|
,
а по таблицам критических точек распределения Стьюдента при и 
найдем 
. Поскольку 
, считаем полученное значение коэффициента корреляции значимым.
Выборочное корреляционное отношение
Рассмотренный ранее выборочный коэффициент корреляции является показателем тесноты корреляционной связи только в том случае, когда эта связь носит линейный характер. Однако существует показатель тесноты корреляционной связи любого характера, в том числе и линейного.
Выборочным корреляционным отношением Y к Х называется отношение межгруппового среднего квадратического отклонения к общему среднему квадратическому отклонению величины Y, т.е.:
,
где межгрупповое среднее квадратическое отклонение определяется формулой:
,
а общее среднее квадратическое отклонение – формулой:
,
где, в свою очередь, групповые средние определяются по формуле:
.
Межгрупповая дисперсия определяет ту часть общей дисперсии величины Y, которая обусловлена изменчивостью величины Х. Поэтому, чем теснее связь, тем большее влияние на вариацию Y оказывает изменчивость Х и, следовательно, тем большие значения принимает выборочное корреляционное отношение.
Перечислим основные свойства выборочного корреляционного отношения:
|
|
|
1. Выборочное корреляционное отношение удовлетворяет двойному неравенству 
.
2. Если 
, то корреляционная связь между Y и Х отсутствует.
3. Если 
, то между Y и Х существует функциональная зависимость.
4. Выборочное корреляционное отношение не меньше модуля выборочного коэффициента корреляции, т.е. 
.
5. Если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, то имеет место линейная корреляционная связь между Y и Х.
ПРИМЕР: По данным таблицы 2.1 подраздела 2.5.1 найти выборочное корреляционное отношение.
Вначале по соответствующим формулам найдем групповые средние и общую среднюю:
Затем найдем межгрупповую и общую дисперсии:
Наконец, найдем выборочное корреляционное отношение:
.
Поскольку найденное выборочное корреляционное отношение практически равно значению выборочного коэффициента корреляции, найденному в примере предыдущего подраздела 
, корреляционную связь следует считать линейной.
Линейная регрессия
Пусть в генеральной совокупности имеются две случайные величины X и Y, и пусть в результате формирования выборки получены n пар чисел 
. Поскольку есть некоторые основания полагать, что связь между этими величинами носит линейный характер, будем искать линейное выборочное уравнение регрессии Y на X в виде: 
.
|
|
|
Для определения параметров a и b используем систему нормальных уравнений по методу наименьших квадратов [6]:
Учитывая справедливость равенств:
решение этой системы можно записать в виде:
Коэффициент b в уравнении регрессии принято называть коэффициентом регрессии Y по Х и обозначать 
. Можно показать, что коэффициент регрессии связан с выборочным коэффициентом корреляции соотношением:
.
Линейное уравнение регрессии в математической статистике принято записывать в следующей форме:
.
Дата добавления: 2018-06-01; просмотров: 431; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!