Сравнение нескольких средних методом дисперсионного анализа
Вернемся теперь к сформулированной в подразделе 2.4.1 задаче: при заданном уровне значимости проверить нулевую гипотезу о равенстве нескольких средних (назовем их групповыми средними) нормальных генеральных совокупностей с неизвестными, но одинаковыми, дисперсиями.
Пусть нулевая гипотеза о равенстве групповых средних верна. Тогда исправленные факторная и остаточная дисперсии, являющиеся несмещенными оценками одной и той же неизвестной генеральной дисперсии (одинаковой для всех групп), будут различаться незначимо. Если сравнить эти оценки с помощью критерия Фишера-Снедекора (см. подраздел 2.3.3), то критерий укажет, что нулевую гипотезу о равенстве факторной и остаточной дисперсий следует принять. Таким образом, если гипотеза о равенстве групповых средних верна, то верна и гипотеза о равенстве факторной и остаточной дисперсий.
Пусть нулевая гипотеза о равенстве групповых средних не верна. Тогда по мере возрастания расхождений между групповыми средними будет возрастать и факторная дисперсия, а вместе с ней будет возрастать и ее отношение к остаточной дисперсии, т.е. величина: 
. В итоге окажется, что 
и, следовательно, гипотеза о равенстве факторной и остаточной дисперсии будет отвергнута.
Таким образом, чтобы проверить нулевую гипотезу о равенстве групповых средних нескольких нормальных генеральных совокупностей с неизвестными, но одинаковыми, дисперсиями, достаточно проверить с помощью критерия Фишера-Снедекора нулевую гипотезу о равенстве факторной и остаточной дисперсий.
|
|
|
При этом, если нулевая гипотеза о равенстве факторной и остаточной дисперсии верна, то случайная величина 
, называемая дисперсионным отношением и определяемая формулой:
,
имеет распределение Фишера-Снедекора с 
и 
степенями свободы. Проверка этой гипотезы осуществляется по методике подраздела 2.3.3.
Пусть известно, что фактор 
оказывает влияние на результативный признак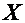 
. Для измерения степени этого влияния используют выборочный коэффициент детерминации, равный:
.
Он показывает, какая доля общей дисперсии объясняется зависимостью результативного признака 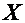от фактора .
ПРИМЕР: В таблице приведены данные по объемам работ, выполненных за смену для четырех бригад. Для приведенных данных для уровня значимости 0,05 проверьте нулевую гипотезу о равенстве групповых средних: 
.
Номер бригады 
| Объем выполненной работы | 
| 
|
| 1 | 140 144 142 145 | 142,75 | 3,69 |
| 2 | 150 149 152 152 | 150,25 | 1,19 |
| 3 | 148 149 146 147 | 147,50 | 1,25 |
| 4 | 150 155 154 152 | 152,75 | 3,69 |
Для проверки нулевой гипотезы вычислим суммы 
и 
, для чего вначале вычислим общую выборочную среднюю:
|
|
|
.
Затем:
Теперь найдем соответствующие исправленные дисперсии:
и наблюдаемое значение критерия Фишера-Снедекора:
.
По таблицам критических точек распределения Фишера-Снедекора для 
и степеней свободы 
найдем 
. Поскольку , нулевую гипотезу отвергаем, т.е. объем ежедневной сменной выработки зависит от работающей бригады. Оценим степень этой зависимости с помощью коэффициента детерминации. Для этого найдем: 
и вычислим:
.
Полученный результат означает, что 84,9% общей вариации ежедневного объема выработки связано с работающей бригадой.
Рекомендуемая литература по теме 2.4:[1 ÷ 4].
ВОПРОСЫ для самопроверки знаний по теме 2.4:
1. На какие слагаемые разбивается общая сумма квадратов отклонений в модели дисперсионного анализа?
2. Какой критерий используется для проверки гипотезы о равенстве групповых средних в дисперсионном анализе?
____________________________________________________________
3. Какой величиной измеряется степень влияния фактора на результативный признак?
____________________________________________________________
Дата добавления: 2018-06-01; просмотров: 439; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!