Несколько мыслей по поводу этого главного урока
· Интегрированный главный урок. Тщательно спланированная, эта трехнедельная эпоха может включать введение в проценты, экономику, формулы (алгебра) и графики.
· Экономика. Для проведения уроков по данной теме, я рекомендую вам познакомиться с книгой Эрнста Шуберта «Уроки математики для шестого класса».
· Того, что здесь перечислено, слишком много для одного главного урока, поэтому изучение процентов необходимо будет продолжить на уроках-упражнениях.
Ключи к успеху в теме проценты
· Обратите внимание учеников, что проценты – это особая дробь со знаменателем 100
· Также покажите, что мы всегда легко можем преобразовать десятичную дробь в проценты, передвигая десятичную запятую на 2 символа вправо (например, 0,71 = 71%). Это объясняется тем, что мы переводим десятичную дробь в дробь со знаменателем 100, то есть мы, по сути, умножаем числитель и знаменатель на 100, а это сдвигает десятичную запятую вправо на 2 символа.
· Не усложняйте! Если вы будете слишком много заниматься процентами в шестом классе, то ученики всё не усвоят. Наша цель – заложить фундамент для дальнейшего изучения в седьмом и восьмом классах.
· Задавайте много задач, которые можно достаточно легко решить в уме, оставьте сложные вычисления до 7 или 8 класса.
· Отложите «странные» проценты (200%, 12,53%, 0,04%) до седьмого класса.
· Не вводите формулы сразу после знакомства с понятием процентов, сначала дайте ученикам время, чтобы выработать чувство процента.
· Не полагайтесь на наглядность (например, на представление о цилиндре, заполненном на 80%), чтобы помочь детям «понять» проценты.
- (см. также «Разделение формы и числа» во Введении)
· Если у учеников возникли сложности с решением задачи, напомните им, что процент – это количество частей на одну сотню (цент), а затем дайте им попробовать еще раз.
· Давайте некоторые ответы в графическом виде (например, круговой график или гистограмма).
Перевод процентов в обычные дроби
(вычислить и запомнить)
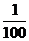 = 1% = 1%
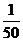 = 2% = 2%
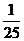 = 4% = 4%
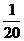 = 5% = 5%
| 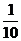 = 10% = 10%
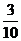 = 30% = 30%
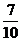 = 70% = 70%
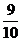 = 90% = 90%
| 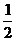 = 50% = 50%
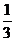 = 33 = 33 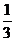 % %
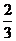 = 66 = 66 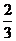 % %
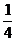 = 25% = 25%
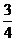 = 75% = 75%
| 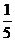 = 20% = 20%
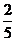 = 40% = 40%
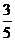 = 60% = 60%
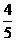 = 80% = 80%
| Не видно |
Нахождение конкретного процента от заданного числа
· Я даю ученикам три способа решения этой задачи. Ученики должны сами выбрать наиболее подходящий способ в каждом конкретном случае.
- Рассмотрение задачи как задачи на деление. (Самый важный способ!)
Такой способ преобразования задачи на проценты в задачу на деление работает только для вычисления следующих процентов:
50% (делим на 2), 33% (делим на 3), 25% (делим на 4), 20% (делим на 5), 10% (делим на 10), 1% (делим на 100).
Пример: Сколько будет 25% от 320?
Решение: Поняв, что 25% это 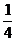 , т.е. мы перефразируем задачу в «Сколько будет
, т.е. мы перефразируем задачу в «Сколько будет 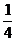 от 320?», что есть, по сути, задача деления 320
от 320?», что есть, по сути, задача деления 320 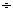 4 = 80.
4 = 80.
- Перевод в обыкновенную дробь и умножение.
Пример: Сколько будет 80% от 350?
Решение: т.к. 80% это 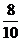 , мы получаем
, мы получаем 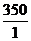 ⋅
⋅ 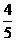 = 280
= 280
- Перевод в десятичную дробь и умножение.
Пример: сколько будет 31% от 62?
Решение: 0,31 ⋅ 62 = 19,22.
· Не слишком акцентируйте внимание на этом способе, т.к. ученики могут в итоге начать пользоваться только им для решения всех задач на проценты.
· Уделите особое внимание тому, чтобы ученики не использовали этот способ там, где гораздо легче решить задачу первым или вторым способом. Например: сколько будет 25% от 320?
Дата добавления: 2018-06-01; просмотров: 249; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
