Преобразование обыкновенных дробей в десятичные
· Преобразуйте обыкновенную дробь в десятичную с помощью деления.
· Для начала не используйте примеры, где ответом будет периодическая десятичная дробь, затем можно включать и такие задачи тоже (см. далее «Периодические дроби»). В каждом случае выполняем деление числителя на знаменатель.
Примеры:  = 0,375;
= 0,375;  = 0,3125;
= 0,3125;  = 0,775.
= 0,775.
· Запомните следующие важные преобразования обыкновенных дробей в десятичные:
Замечание: скобки в дробной части означают период, т.е. число, находящееся в скобках повторяется (5,(372) означает 5,372372372…)
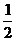 = 0.5; = 0.5;
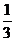 = 0,(3); = 0,(3);
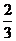 = 0,(6); = 0,(6);
 = 0,25; = 0,25;
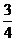 = 0,75; = 0,75;
| 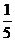 = 0,2; = 0,2;
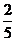 = 0,4; = 0,4;
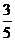 = 0,6; = 0,6;
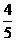 = 0,8; = 0,8;
|  = 0,1(6) ; = 0,1(6) ;
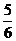 = 0,8(3); = 0,8(3);
| 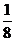 = 0,125; = 0,125;
 = 0,375; = 0,375;
 = 0,625; = 0,625;
 = 0,875; = 0,875;
|  = 0,(1); = 0,(1);
 = 0,(2); = 0,(2);
 = 0,(4); = 0,(4);
 = 0,(5); = 0,(5);
 = 0,(7); = 0,(7);
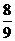 = 0,(8). = 0,(8).
|
· Способ преобразования дробей со знаменателем 11 и 20.
· Ученикам не нужно заучивать эти преобразования наизусть, но они должны уметь легко делать их в уме.
· Дроби со знаменателем 11: умножьте числитель на 9 и получите период нужной нам десятичной дроби.
· Дайте ученикам несколько примеров ( 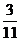 ,
,  ,
,  ), возможно, они смогут вывести правило преобразования самостоятельно.
), возможно, они смогут вывести правило преобразования самостоятельно.
Пример: преобразовать  в десятичную дробь.
в десятичную дробь.
Решение: вместо того, чтобы делить 4 на 11, мы можем умножить 4 на 9, и получить 0,(36)
· Дроби со знаменателем 20. Умножьте числитель на 5, поместите ответ в дробную часть десятичной дроби без повторения. Удобный приём здесь – «мыслить в пятаках», так как пятак – это 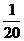 рубля. Например,
рубля. Например, 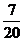 – это 7 пятаков, что равняется 35 копейкам, или 0,35 рубля.
– это 7 пятаков, что равняется 35 копейкам, или 0,35 рубля.
|
|
|
Пример: преобразовать 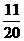 в десятичную дробь.
в десятичную дробь.
Решение: умножим 11 на 5, получим ответ 0,55
Преобразования десятичных дробей в обыкновенные
· Просто запишите дробь со знаменателем 10, 100, 1000 и т.д. и сократите её.
Пример: представить 0,075 в виде обыкновенной дроби.
Решение: запишем дробь  , после сокращения получим
, после сокращения получим  .
.
Периодические дроби
· Более подробно периодические дроби рассмотрены в Приложении B, «Вопросы о периодических дробях»
· Обратите внимание учеников, что задача деления зацикливается, когда остаток от деления появляется второй раз.
· Несмотря на то, что любая задача на деление будет иметь результат, конечный или повторяющийся, вы должны заранее проверить, что период будет содержать не слишком много знаков перед тем, как давать задачу ученикам
· (Только для учителя) Как определить, сколько знаков будет в периоде.
· Информация ниже пригодится, потому что, встречая задачу с ответом в виде периодической дроби, вы сможете оценить, насколько эта задача трудна, глядя на делитель.
· Вспомним, что любая задача на деление может быть представлена в виде дроби, где числитель мы делим на знаменатель. Если считать, что наша дробь уже приведена к сокращенному виду, то количество знаков в периоде зависит только от ее знаменателя (делителя).
|
|
|
· Ниже перечислены разные делители и то, сколько знаков в периоде они дают:
- В результате деления на следующие делители получается конечная десятичная дробь. (Обратите внимание, что для этих чисел в разложении на простые множители участвуют только степени 2 и 5. См. «Арифметика 6 класс», Другие разделы: Разложение на простые множители):
2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, 100…
- В результате деления на следующие делители получается десятичная дробь с периодом, содержащим 1 знак. (Обратите внимание, что для этих чисел в разложении на простые множители участвуют 3 или 32 , а также 2 и 5 в некоторых степенях):
3, 6, 9, 12, 15, 18, 24, 30, 36, 45, 48, 60…
- В результате деления на следующие делители получается десятичная дробь с двумя знаками в периоде: 11, 22, 33, 44, 55, 66, 88, 99…
- В результате деления на следующие делители получается десятичная дробь с 3 знаками в периоде: 37, 74, 111… и 27, 54 (не 81).
· В результате делении на следующие делители получается десятичная дробь с 4 знаками в периоде: 101, 202, 303… и 1111, 2222…
- В результате делении на следующие делители получается десятичная дробь с 5 знаками в периоде: 41, 82, 123… и 271, 542…
- В результате делении на следующие делители получается десятичная дробь с 6 знаками в периоде: 7, 14, 21… и 13, 26, 39…, а также 143, 259. 297, 351, 407, 481…
- В результате делении на следующие делители получается десятичная дробь с 7 знаками в периоде: 239, 478… и 4649, 9298…
- В результате делении на следующие делители получается десятичная дробь с 8 знаками в периоде: 73, 146… и 137, 274…
- В результате делении на следующие делители получается десятичная дробь с 9 знаками в периоде: 81, 162… и 333667 (на самом деле!).
Пример: 8 ∶ 37 = 0,(216)
|
|
|
Пример: 173 ∶ 808 = 0,214(1089)
Пример: 39 ∶ 64 = 0,609375 (не периодическая дробь).
- Если делитель представляет собой число, состоящее из одинаковых цифр, то результатом деления будет периодическая дробь, имеющая в периоде столько же знаков, сколько цифр в делителе (правило не распространяется на делители с цифрой 7). Например, поделим 273956 на 88888. Мы знаем, что ответом будет периодическая дробь с периодом в 5 знаков, т.к. делителем является число, состоящее только из цифры восемь, и эта цифра повторяется пять раз.
· В следующих примерах мы выполняем деление столбиком и делим числитель на знаменатель:
Пример: 871 ∶ 1111=0,(7839)
Пример: 179 ∶ 444=0,40(313).
|
|
|
Дата добавления: 2018-06-01; просмотров: 683; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
