Графические характеристики выборки
Такими характеристиками служат эмпирическая функция распределения, полигон частот (относительных частот) и гистограмма.
Эмпирической функцией распределения 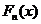 называется относительная частота того, что признак (случайная величина Х) примет значение, меньше заданного х,т.е.
называется относительная частота того, что признак (случайная величина Х) примет значение, меньше заданного х,т.е.
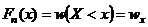
Полигон частот – ломаная, концы отрезков которой имеют координаты 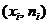 или
или 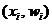 - для полигона относительных частот. Полигон частот используется для графического представления простого статистического ряда.
- для полигона относительных частот. Полигон частот используется для графического представления простого статистического ряда.
Гистограмма служит для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру, состоящую из прямоугольников с основаниями, равными интервалам значений признака 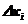 и высотами
и высотами 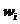 . Площадь всей гистограммы равна 1. На рисунке 8.1 изображен полигон частот, на рисунке 8.2 - эмпирическая функция распределения, на рисунке 8.3 – гистограмма для примера 1.
. Площадь всей гистограммы равна 1. На рисунке 8.1 изображен полигон частот, на рисунке 8.2 - эмпирическая функция распределения, на рисунке 8.3 – гистограмма для примера 1.
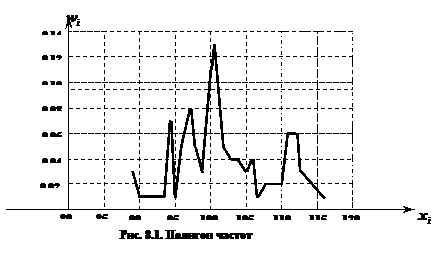




Точечные характеристики выборки (оценки параметров)
Вариационный ряд является статистическим аналогом (реализации) распределения признака (случайной величины Х). В этом смысле полигон (гистограмма) аналогичен кривой распределения - дифференциальной функции распределения случайной величины Х. Однако построение их достаточно громоздко. В то же время, на практике часто оказывается достаточным знание лишь числовых характеристик случайной величины (признака Х)- математического ожидания, дисперсии и т.д. Но числовые характеристики Х неизвестны и информация о них может быть получена только на основе изучения имеющихся опытных данных – выборки. В математической статистике принято говорить, что некоторые сводные характеристики выборки служат для оценивания (являются оценкой) числовых характеристик генеральной совокупности. Эти характеристики носят название точечных оценок выборки. Расчет их – следующий этап обработки опытных данных.
|
|
|
К точечным оценкам предъявляются требования несмещенности, состоятельности и эффективности.
Оценка 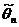 параметра
параметра 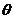 генеральной совокупности называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.
генеральной совокупности называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е.
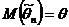 .
.
Оценка 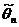 параметра генеральной совокупности
параметра генеральной совокупности 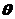 называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
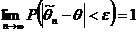 .
.
Эффективной называется та оценка, которая имеет наименьшую дисперсию среди других возможных оценок.
Рассмотрим эти оценки.
Выборочная средняя – (аналог математического ожидания с.в.) -средняя арифметическая значений вариант, рассчитанная по значениям вариационного ряда:
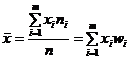 (8.3.1),
(8.3.1),
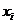 - варианты простого статистического ряда или середины интервалов вариационного;
- варианты простого статистического ряда или середины интервалов вариационного; 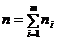 .
.
|
|
|
Выборочная дисперсия – (аналог дисперсии с.в.) - средняя арифметическая квадратов отклонения вариант от выборочной средней; служит характеристикой рассеяния вариант относительно выборочной средней:
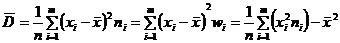 (8.3.2.).
(8.3.2.).
Выборочная дисперсия не удовлетворяет свойству несмещенности, поэтому вводится также исправленная выборочная дисперсия:
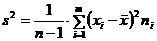 (8.3.3.).
(8.3.3.).
Желательно в качестве меры рассеяния иметь характеристику, выраженную в тех же единицах, что и варианты. Поэтому вводится среднее выборочное квадратическое отклонение:
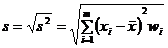 (8.3.4.).
(8.3.4.).
Рассматривается также безразмерная характеристика – коэффициент вариации, который служит для оценки однородности опытных данных:
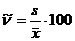 % (8.3.5.).
% (8.3.5.).
Мода 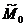 – варианта, которой соответствует наибольшая частота;
– варианта, которой соответствует наибольшая частота;
Медиана 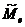 – значение признака, приходящееся на середину вариационного ряда (количество вариант меньших
– значение признака, приходящееся на середину вариационного ряда (количество вариант меньших 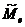 равно количеству вариант больших
равно количеству вариант больших 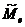 ).
).
Для дискретного ряда из нечетного числа членов медиана равна серединной варианте, для ряда из четного числа членов – полусумме двух серединных вариант.
|
|
|
Рассчитаем эти оценки для примера 1.
4Выборочная средняя:
а) Для простого вариационного ряда (таблица 1):
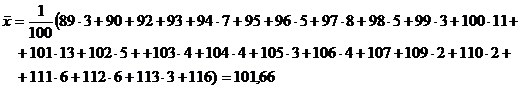
б) Для интервального вариационного ряда (таблица 2):
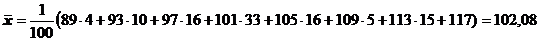
Выборочная дисперсия:
а) Для простого вариационного ряда:
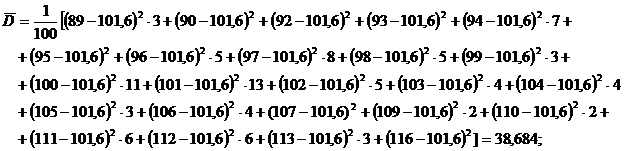
б) Для интервального вариационного ряда;
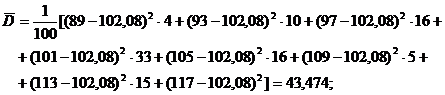
Исправленная выборочная дисперсия и среднее выборочное квадратическое отклонение:
а) Для простого вариационного ряда:
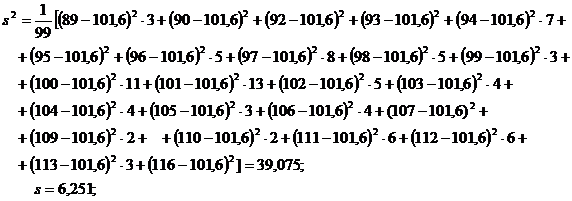 б) Для интервального вариационного ряда;
б) Для интервального вариационного ряда;
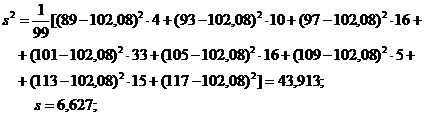
Коэффициент вариации:
а) Для простого вариационного ряда:
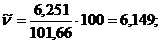
б) Для интервального вариационного ряда;
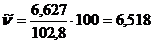
Мода и медиана:
а) Для простого вариационного ряда:
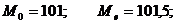
б) Для интервального вариационного ряда;
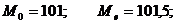 3
3
Дата добавления: 2018-05-13; просмотров: 236; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
