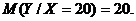Числовые характеристики системы случайных величин
Закон распределения полностью характеризует систему случайных величин, но использовать его на практике не всегда удобно в силу сложности. Зачастую бывает достаточно знать числовые характеристики составляющих систему случайных величин, к которым относятся: математические ожидания M[X], M[Y], дисперсии D[X], D[Y] и среднеквадратические отклонения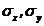 
. Они вычисляются по следующим формулам.
Для дискретных систем случайных величин
; 
; 
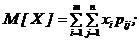
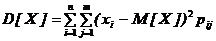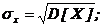
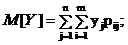
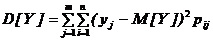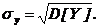
Для непрерывных систем случайных величин
; 
;
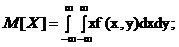
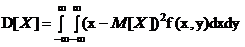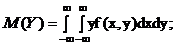
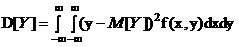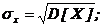
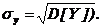
Дисперсии составляющих можно вычислять и по укороченным формулам:
Важную роль в теории двумерных случайных величин играет корреляционный момент (ковариация)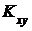 
, характеризующий линейную связьмежду составляющими системы:
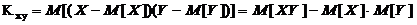. (6.7)
Корреляционный момент вычисляется по следующим формулам.
Для дискретных систем случайных величин
.
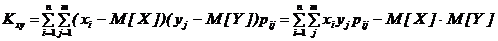Для непрерывных систем случайных величин
= 
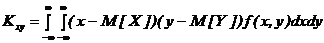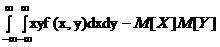
Наряду с корреляционным моментом используется безразмерная характеристика корреляционной связи - коэффициент корреляции
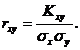(6.8)
Для любых систем случайных величин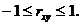 
Случайные величины Х и Y называются некоррелированными, если 
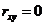.Независимые величинывсегда некоррелированы.
Условным законом распределения случайной величины, входящей в систему, называется закон ее распределения, вычисленный при условии, что другая случайная величина приняла определенное значение. Для систем непрерывных случайных величин условные законы выражаются условными плотностями распределения составляющих:
|
|
|
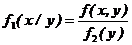, при этом 
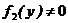, (6.9)
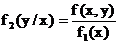, при этом 
.
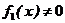Законы равномерного и нормального распределения систем случайных величин
Равномерный закон. Если все значения случайных величин входящих в систему расположены внутри области D, и плотность вероятности системы имеет следующий вид:
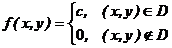и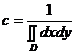 
, (6.10)
то (Х,У) подчинена равномерному закону распределения.
Нормальный закон. Если плотность распределения системы (Х,У) имеет вид
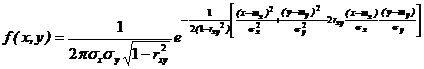, (6.11)
где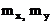 
- математические ожидания; 
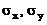- среднеквадратичные отклонения, а 
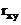- коэффициент корреляции, то система подчинена нормальному закону распределения.
Для некоррелированных случайных величин нормальная плотность распределения имеет вид:
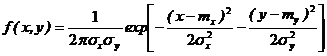. (6.12)
Пример 6.2. Планируется деятельность 3-х предприятий на очередной год. Система (X,Y), где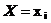 
- номер предприятия, 
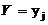-размеры вложений (в тыс. усл. ден. ед.), 
, 
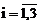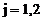, задана таблицей. Построить законы распределения составляющих системы, найти все числовые характеристики системы:
 \ 
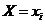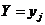
| 3 | 4 |
| 1 | 0,1 | 0,2 |
| 2 | 0,1 | 0,1 |
| 3 | 0,3 | 0,2 |
.4 Законы распределения составляющих системы строим в виде таблиц 2 и 3, суммируя вероятности соответственно по строкам (для составляющей Х) или по столбцам (для составляющей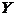 
).
|
|
|
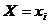
| 1 | 2 | 3 |
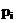
| 0,1+0,2=0,3 | 0,1+0,1=0,2 | 0,3+0,2=0,5 |
Закон распределения составляющей Х означает, что независимо от объема вложений первое предприятие будет иметь вложения с вероятностью 0,3, второе - с вероятностью 0,2 и третье – с вероятностью 0,5. Составляющей Y соответствует закон распределения
|
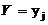
| 3 | 4 |
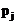
| 0,1+0,1+0,3=0,5 | 0,2+0,1+0,2=0,5 |
и это значит, что независимо от номера предприятия объем вложений может быть равен 3 тыс. усл. ден. ед. с вероятностью 0,5 или 4 тыс. усл.ден.ед. с вероятностью 0,5.
Для определения числовых характеристик составляющих воспользуемся найденными законами распределения Х и Уи формулами для определения числовых характеристик дискретных систем:
; 
; 
.
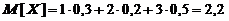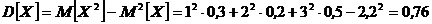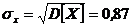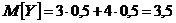- средний объем вложений;
;
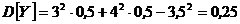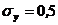- отклонение от среднего объема вложений.
Связь между номером предприятия и объемом вложений:
;
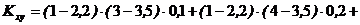
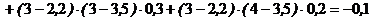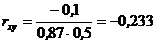. 3
Пример 6.3. На производстве за определенный период использовалось два вида сырья. Случайные величины X и Y – соответственно объемы сырья, выраженные в условных единицах. Плотность распределения вероятностей системы имеет вид:
|
|
|
.
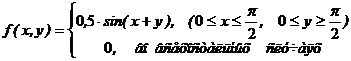Определить: 1) интегральную функцию распределения F(х,у)и числовые характеристик M[X], M[Y], D[X], D[Y], Кху.; 2) вероятность попадания случайной точки (Х, У) в прямоугольник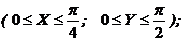 
4F(х,у) находим в соответствии с формулами (6.2)
1) x<0 или y<0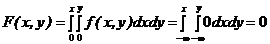 
;
2) 
= 
= 
;
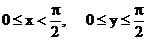
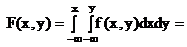
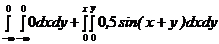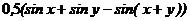3) 
=
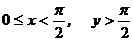
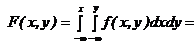
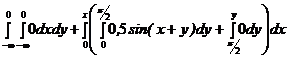=0,5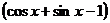 
;
4) 
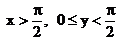
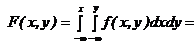
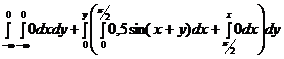= =0,5 
;
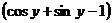5) 
+ 
.
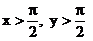
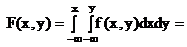
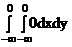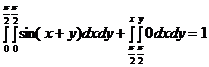Таким образом,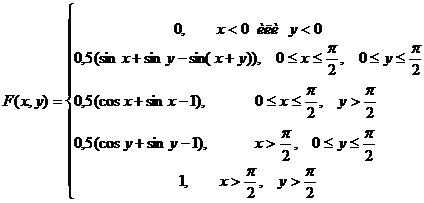 
.
Числовые характеристики M[X], D[X] вычисляются по формулам определения числовых характеристик непрерывных систем:
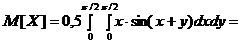
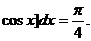
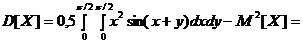
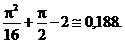
Из симметрии f(x,y) относительно x и y следует, что M[X]=M[Y], D[X]=D[Y].
Корреляционный момент: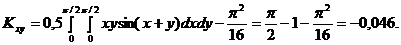 
Вероятность попадания (Х,У) в прямоугольник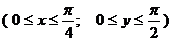 
в соответствии с формулой (6.4)
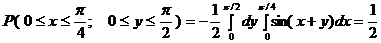. 3
Задачи
6.1. Система (Х, У) задана законом распределения:
| X \ Y | 10 | 20 | 30 |
| 10 | 0,1 | 0,05 | 0,02 |
| 20 | 0,1 | 0,3 | 0,1 |
| 30 | 0,2 | 0,1 | 0,03 |
Найти: M[X], M[Y], M[X/Y=10],
Ответ: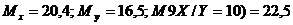
.
6.2. Фирма предлагает 3 варианта проекта двум строительным организациям. Таблицей задан закон распределения системы (Х, У), где Xi-номер проекта, Yj-номер организации, pij- вероятности принятия j–той организацией i-того проекта:
| X \ Y | 1 | 2 |
| 1 | 0,1 | 0,2 |
| 2 | 0,3 | 0,2 |
| 3 | 0,1 | 0,1 |
Определить числовые характеристики системы
Ответ: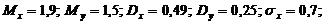 
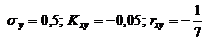
6.3. Из коробки, в которой 4 красных, 2 синих и 3 зеленых карандаша, наудачу извлекли 3 карандаша. Пусть Х- число красных, а У- число синих карандашей среди извлеченных. Найти: а) закон распределения системы (Х,У); б) законы распределения составляющих Х и У; в) вероятность события (Х<3,У=2).
|
|
|
Ответ: а, б)
| X\Y | 0 | 1 | 2 | 
|
| 0 | 1/84 | 6/84 | 3/84 | 10/84 |
| 1 | 12/84 | 24/84 | 4/84 | 40/84 |
| 2 | 18/84 | 12/84 | 0 | 30/84 |
| 3 | 4/84 | 0 | 0 | 4/84 |
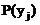
| 35/84 | 42/84 | 7/84 | 1 |
в)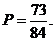 
6.4. Два стрелка независимо друг от друга сделали по выстрелу в одну и ту же мишень. Вероятность попадания для первого стрелка 0,8; для второго- 0,6. Пусть Х- число попаданий первого стрелка, а У- число попаданий второго. Найти: а) законы распределения составляющих Х и У; б) закон распределения системы (Х,У). в) зависимы или нет случайные величины Х и У.
| Х\У | 0 | 1 |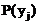 
|
| 0 | 0,08 | 0,32 | 0,4 |
| 1 | 0,12 | 0,48 | 0,6 |
|
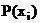
| 0,2 | 0,8 | 1 |
Ответ:а, б):
в) независимы.
6.5. Система задана законом распределения:
| X \ Y | -1 | -2 | -3 |
| 1 | 0,2 | 0,1 | 0,1 |
| 2 | 0,4 | 0,1 | 0,1 |
найти: M[X], M[Y], D[X], D[Y], Kxy.
Ответ: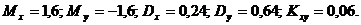
6.6. Дважды брошена игральная кость. Пусть Х – количество выпавших очков при первом бросании, а У – сумма выпавших очков в обоих бросках. Найти M[X], M[Y].
Ответ: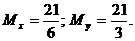
6.7. Система случайных величин (X,Y)распределена равномерно внутри прямоугольника, ограниченного прямыми: x=1; x=3; y=0; y=2. Найти D[X], D[Y].
Ответ: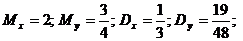
6.8. Система (X;Y) задана плотностью распределения вероятности:
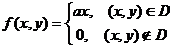, где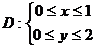 
. Найти М[X], М[Y].
Ответ: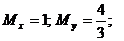
6.9. Система (X;Y) задана плотностью распределения вероятностей
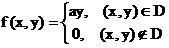где D: 0 £ х £ 2; 0 £ у £ 2. Найти М[X], М[Y].
Ответ: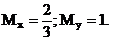
6.10. Система (X;Y) распределена равномерно в области D: {у = х + 3; у = х; х = 0; х = 4}. . Найти М[X], М[Y].
Ответ: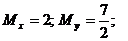
6.11. Система (X;Y) распределена равномерно в области D: {у = х; у + 3х= 4; у = 0}. Найти М[X], М[Y].
Ответ: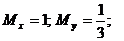
6.12. Система (Х;У) распределена равномерно в области D:{ у = х/2; х = 4; у = 4; х = 0}. Найти М[X], М[Y].
Ответ: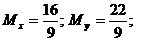
6.13. Коэффициенты b и с квадратного уравнения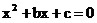 
наудачу и независимо друг от друга выбираются на отрезке [0; 2]. Найти вероятность того, что корни этого уравнения окажутся действительными.
Ответ: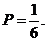
| X \ Y | -10 | 0 | 10 |
| -5 | 0,05 | 0,30 | 0,15 |
| 5 | 0,20 | 0,05 | 0,25 |
6.14. Система дискретных случайных величин X и Y задана законом распределения:
Найти корреляционный момент Kxy.
Ответ: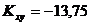 
.
6.15. Система случайных величин (X,Y) распределена равномерно внутри треугольной области D, ограниченной прямыми: x=0, y=0 и x+y-1=0. Найти двумерную плотность распределения вероятностей f(x,y) системы.
Ответ: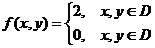
6.16. Система случайных величин (Х,Y) задана двумерной плотностью вероятностей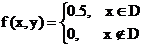 
, где область 
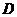ограничена прямыми 
, 
, 
, 
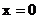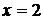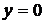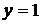. Найти корреляционный момент 
.
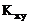Ответ: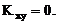
6.17. Система дискретных случайных величин X и Y задана законом распределения:
| X \ Y | -1 | -2 |
| 1 | 0,1 | 0,2 |
| 2 | 0,3 | 0,2 |
| 3 | 0,1 | 0,1 |
Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Y.
Ответ: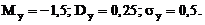
6.18. Система дискретных случайных величин X и Y задана законом распределения:
| X \ Y | 10 | 20 | 30 |
| 10 | 0,1 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 | 0,2 |
Найти а) условный закон распределения случайной величины Y и б) условное математическое ожидание my/x при условии, что X =20.
| Ответ: а) | У/Х=2 | 10 | 20 | 30 | б) |
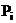
| 1/5 | 3/5 | 1/5 |
6.19. Система дискретных случайных величин X и Y задана рядом распределения:
| X \ Y | 10 | 20 | 30 |
| 10 | 0,1 | 0,05 | 0,2 |
| 20 | 0,1 | 0,03 | 0,1 |
| 30 | 0,2 | 0,02 | 0,2 |
Найти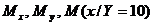 
.
Ответ: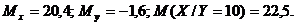
6.20. Система дискретных случайных величин X и Y задана законом распределения:
| X \ Y | -3 | 4 |
| ‑3 | 0,1 | 0,2 |
| 2 | 0,1 | 0,1 |
| 3 | 0,3 | 0,2 |
Найти корреляционный момент Kxy.
Ответ -3,1
6.21. Система случайных величин X и Y распределена равномерно в прямоугольной области, ограниченной прямыми линиями: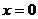 
, 
, 
, 
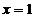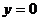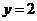. Найти одномерную плотность распределения 
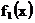и математическое ожидание величины Х.
Ответ: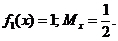
6.22. Система дискретных случайных величин X и Y задана законом распределения:
| X \ Y | 1 | 2 | 3 |
| ‑3 | 0,2 | 0,1 | 0,2 |
| ‑4 | 0,3 | 0,1 | 0,1 |
Найти: а) условный закон распределения случайной величины Y и б) условное математическое ожидание my/x при условии, что X= ‑3.
| Ответ: а)
| 
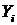
| 1 | 2 | 3 |
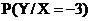
| 0,4 | 0,2 | 0,4 |
б)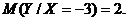 
6.23. Система дискретных случайных величин X и Y задана законом распределения:
| X \ Y | 20 | 30 | 40 |
| ‑1 | 0,3 | 0,1 | 0,1 |
| ‑2 | 0,1 | 0,3 | 0,1 |
Найти корреляционный момент Kxy.
Ответ: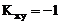 
6.23. Рассматривается двумерная случайная величина (Х,У), где Х – поставка сырья, У – поступление требований на него. Известно, что поступление сырья и требований на него могут произойти в любой день месяца (30 дней) с равной вероятностью. Найти: а) выражения для совместной плотности (Х,У); б) плотности вероятности составляющих системы; в) зависимы или независимы Х и У?
Ответ: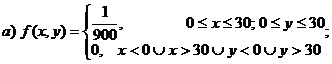 
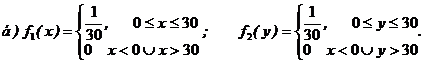
6.24. Найти плотность вероятности случайной величины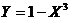 
, если Х распределена по закону Коши с плотностью вероятностей 
.
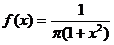Ответ: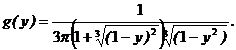
Дата добавления: 2018-05-13; просмотров: 769; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!