Глава 5. Наиболее распространенные законы распределения случайных величин и их числовые характеристики

Биномиальное распределение

СВ Х распределена по биномиальному закону, если она принимает значения 0, 1, 2, …, n, а соответствующие вероятности вычисляются по формуле Бернулли:

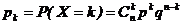, (5.1)

где 0 < p < 1, q=1 - p, k=0, 1, 2, …, n.

Такая СВ выражает число появлений события А в п независимых испытаниях, проводимых в одинаковых условиях.

Ряд распределения имеет вид:

х_i=k

…

P(X=k)

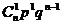
А числовые характеристики равны:

D[X]=npq. (5.2)

Пример 5.1. Три конкурирующие фирмы работают независимо друг от друга. Вероятность обанкротиться для каждой из них равна 0.1. Составить закон распределения СВ Х – числа обанкротившихся фирм. Найти математическое ожидание и дисперсию Х.

4Дискретная СВ X - число обанкротившихся фирм имеет следующие возможные значения: x₁=0 (ни одна фирма не обанкротилась), x₂=1 (обанкротилась одна фирма), x₃=2 (две обанкротились) и x₄=3(обанкротились все три). Банкротства фирм независимы друг от друга, поэтому применима формула Бернулли ( n=3, k=0, 1, 2, 3; p=0,1, q=1 ‑ 0,1= 0,9 ), следовательно,

P(X=0)=P₃(0)=q³=0,9³=0,729; P(X=1)=P₃(1)= pq²=3´0,1´0,9=0,243;

P(X=2)=P₃(2)= p²q=3´(0,1)²´(0,9)=0,027; P(X=3)=P₃(3)=p³=0,1³=0,001.

Контроль: 0,729+0,243+0,027+0,001=1.

` Закон распределения Х имеет вид:

х_i=k	0	1	2	3
P(X=k)	0,729	0,243	0,027	0,001

M[X]= ; D[X]= . 3

Геометрическое и гипергеометрическое распределения

Дискретная СВ Х подчинена геометрическому распределению, если ее возможные значения 0, 1, 2, …, k, …, асоответствующие вероятности можно вычислить по формулам:

(5.3)

где 0 <p <1, q=1 - р.

x_i	0	1	2	…	k	…
p_i	p	pq	pq²	…	pq^k	…

Ряд распределения Х имеет вид:

Математическое ожидание и дисперсия соответственно равны:

D[X] . (5.4)

СВ Хподчинена гипергеометрическому распределению с параметрами a, b, n, если ее возможные значения 0, 1, 2, …, k, …, а, а соответствующие вероятности вычисляются по формулам:

, . (5.5)

(Если в урне а белых и b черных шаров и из нее вынимают n шаров, то СВ Х={число белых шаров среди вынутых} подчиняется гипер-геометрическому закону).

Примечание. В приведенной формуле полагают , если .

Математическое ожидание и дисперсия гипергеометричекого распределения: ,

D . (5.6)

Пример 5.2. В группе 20 студентов, среди которых 8 отличников. По списку наудачу отобраны 5 студентов. Найти закон распределения и построить функцию распределения F(x) СВ Х - числа отличников среди отобранных студентов. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение Х.

4СВ Х ‑ число отличников среди отобранных студентов ‑ принимает возможные значения: 0, 1, 2, 3, 4, 5.

, ,

, .

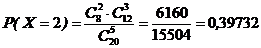=0,05108+0,25524+0,39732+0,23839+0,05418+0,02167=1

Ряд распределения имеет вид:

	0	1	2	3	4	5
	0,05108	0,25524	0,39732	0,23839	0,05418	0,02167

Построим функцию распределения СВ Х:

при х <0 F(x)=0;

0£ х <1 F(х)=0,05108;

1£ х <2 F(x)=0,05108+0,25542=0,30650;

2£ х<3 F(x)=0,05108+0,25542+0.39732=0,70382.

3£ х <4 F(x)= 0,05108+0,25542+0.39732+0,23839=0,94221.

4£ х <5 F(x)= 0,05108+0,25542+0.39732+0,23839+0,05418=0,99639.

х ³ 5 F(x)= 0,05108+0,25542+0.39732+0,23839+0,05418+0,02167=1.

Математическое ожидание, дисперсия, среднее квадратичное отклонение по формулам 5.6. соответственно равны:

M[X]= =2; D[X]= =1,45;

. 3

Распределение Пуассона

СВ Х распределена по закону Пуассона, если онапринимает целые неотрицательные значения: 0, 1, 2, …, k, …, вероятности которых можно вычислить по формулам:

, (5.7)

где k – число появлений событияАв n независимыхиспытаниях ( 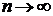), ( )‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то .

Распределение Пуассона является предельным для биномиального распределения, когда число испытаний n достаточно велико, а вероятность р появления события в каждом испытании мала (порядка 1/n).

Ряд распределения СВ Х , распределенной по закону Пуассона, имеет вид:

х	0	1	2	…	n	…
р_k				…		…

Математическое ожидание и дисперсия соответственно равны:

, D . (5.8)

Типичными примерами случайных величин, подчиняющихся распределению Пуассона, являются: число вызовов на телефонной станции за некоторое время t; число отказов аппаратуры за время t, если известно, что отказы независимы друг от друга и в среднем на единицу времени приходится l отказов, и т.д.

Пример 5.3.На телефонную станцию в течение часа поступают в среднем 30 вызовов. Найти вероятность того, что в течение минуты поступает не более двух вызовов.

4Математическое ожидание числа вызовов за минуту равно . Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:

P(k£2) = p(X=0)+P(X=1)+P(X=2)= = + + = (1+1/2+ )»0,98. 3

Равномерное распределение

СВ Х подчинена равномерному закону распределения, если ее плотность распределения вероятностей имеет вид:

. (5.9)

График плотности равномерного распределения f(x) изображен на рис.5.1.

Интегральная функция распределения F(x) равна: , (5.10)

ее график изображен на рис. 5.2.

Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:

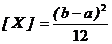; D ; . (5.11)

Вероятность попадания Х в заданный интервал значений определяется: .

Пример 5.4 Цена деления измерительного прибора равна 0,1. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02.

4Ошибку округления можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. В рассматриваемой задаче длина интервала, в котором заключены возможные значения Х, равна 0,1, отсюда:

Очевидно, ошибка превысит 0,02, если 0,02<X<0,08. Вероятность

. 3

Показательное распределение

Непрерывная СВ Х распределена по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей имеет вид:

, (5.12)

где l - параметр распределения.

Кривая плотности распределения f(x)изображена на рис.5.3. Интегральная функция распределения равна

, (5.13)

ее график показан на рис 5.4.

Математическое ожидание, дисперсия и среднее квадратичное соответственно равны:

M[X]=1/l; D[X]=1/l²; s_х=1/l; (5.13)

а вероятность попадания Х в заданный интервал значений определяется следующим образом: .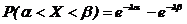

Пример 5.5.СВ Т—время безотказной работы телевизора - имеет показательное распределение. Определить вероятность того, что время безотказной работы телевизора будет не меньше 600 часов, если среднее время работы его 400 часов.

4 По условию задачи математическое ожидание СВ Т равно 400 часов. Искомая вероятность

P(T ³ 600 )= 1- P(T<600 )= 1- F(600)=1-(1-e^-^600/400)=e^-1,5» 0,2231. 3

Нормальное распределение

СВ Х подчинена нормальному закону распределения,если ее плотность распределения вероятностей имеет вид:

, (5.14)

где a ‑ математическое ожидание, ‑ среднее квадратичное отклонениеХ.

Интегральная функция нормального распределения имеет вид

; (5.15)

где - функция Лапласа, или интеграл вероятностей.

Основные свойства функции Лапласа:

1) F(0) = 0;

2) (нечетная функция);

3) F(¥)=0,5

Таблица значений функции F(х) для приведена в приложении, поскольку она является нечетной, то для отрицательных значений х пользуются теми же таблицами, что и для положительных.

Вероятность попадания Х в заданный интервал значений :

, (5.16)

Вероятность того, что абсолютная величина отклонения нормальной СВ Х от ее математического ожидания меньше положительного числа d, определяется выражением:

. (5.17)

В частности, при а=0, P(êХ ê<d) =2F(d/s).

Если в равенстве 5.17. взять , получим так называемое «правило трёх сигм», которое является одним из необходимых условий того, что СВ имеет нормальный закон распределения. В самом деле,

т.е. отклонение нормальной СВ от своего математического ожидания а на величину, равную является событием практически достоверным.

Дата добавления: 2018-05-13; просмотров: 563; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 2 3 4 5 678 9 10 11 Следующая ⇒

Мы поможем в написании ваших работ!