Плоскопараллельное движение твердого тела

Плоскопараллельное движение тела можно рассматривать как сумму двух простых движений: поступательного вместе с полюсом и вращательного вокруг полюса. Уравнения плоского (плоскопараллельного) движения твердого тела:

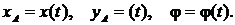
Поступательная часть движения  зависит от выбора полюса А, а вращательная часть движения от выбора полюса не зависит, т. е. ω и e – общие кинематические характеристики движения всего твердого тела в целом.

Теорема.Скоростьлюбой точки плоской фигуры равна геометрической сумме скорости полюса и скорости этой точки в её вращении вместе с фигурой вокруг полюса: если  А – полюс, то скорость любой точки М плоской фигуры по теореме

,

здесь  – скорость точки М в её вращении вместе с фигурой вокруг полюса А (  и ) (рис. 2.26).

Следствия теоремы:

· проекции скоростей точек тела на прямую, проходящую через эти точки, равны;

· концы скоростей точек неизменяемого отрезка лежат на одной прямой и делят эту прямую на части, пропорциональные расстояниям между соответствующими точками отрезка (рис. 2.27).

Рис. 2.27

 

Мгновенный центр скоростей (МЦС)

Теорема. В каждый момент времени при плоском движении тела, если , имеется единственная точка в плоскости его движения, скорость которой равна нулю. Эту точку называют мгновенным центром скоростей (МЦС).

Если эту точку выбрать за полюс, то по теореме при определении скорости точки фигуры поступательная часть движения будет равна нулю, а остается только вращательная часть движения. Таким образом, скорости точек плоской фигуры определяются в данный момент времени так, как если бы движение фигуры было вращением вокруг МЦС.

Рис. 2.28

Если положение МЦС известно, то, приняв МЦС за новый полюс ( ) для любой другой точки тела, например точки А (рис. 2.28), скорость можно вычислить следующим образом:

 

,

здесь АР – расстояние от точки А до МЦС, т. е. до точки Р.

Скорость точки В вычислим аналогично:

.

Из полученных выражений для V_А и V_В имеем

или .                              (2.6)

Следовательно, если положение МЦС известно, то скорости точек тела вычисляют так же, как и в случае вращения тела в плоскости вокруг точки Р с угловой скоростью 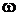 (рис. 2.28).

Рис. 2.29

 

Пример 2.6. Колесо радиусом R катится без скольжения по линейному рельсу. Центр С колеса движется согласно уравнению . Вычислить скорости точек обода колеса Р, М, К, N, расположенных, как показано на рис. 2.29.

 

Решение. Получим уравнения движения колеса. Имеем (рис. 2.29):

.

 

За полюс выберем точку . Вычислим скорость полюса и угловую скорость вращения колеса  вокруг полюса. Имеем:

 

 

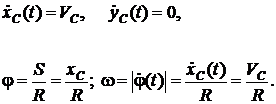
Применим последовательно к точкам Р, К, N, М, лежащим на ободе колеса, теорему о скоростях при плоском движении:

 

.

 

Отметим, что скорости по модулю на ободе колеса при его вращении вокруг условно неподвижного полюса равны между собой (рис. 2.30):

 

.

 Рис. 2.30

 

Направление слагаемых скоростей в исследуемых точках показаны на
рис. 2.31.

1. Точка Р:

здесь ║ , тогда .

2. Точка М: ,

здесь , тогда .

Рис. 2.31

3.  Точка К: ,

здесь ║ , тогда

4. Точка N: ,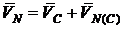

здесь , тогда

.

Отметим, что перпендикуляры, проведенные к векторам скоростей соответственно в точках К, N, М (рис. 2.31), пересекутся в точке , скорость которой равна нулю.

Ответ: V_P = 0, V_M = V_N = , V_K = 2 V_C.

---

Дата добавления: 2018-05-12; просмотров: 696; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!