Вращение твердого тела относительно неподвижной точки в плоскости

⇐ ПредыдущаяСтр 8 из 15Следующая ⇒

Движение точки в плоскости по окружности.Введем радиус-вектор . Совместим начало радиус-вектора с центром окружности О, полярную ось направим по радиусу (рис. 2.10, а). Тогда при движении точки будет меняться только угол между радиус-вектором и осью , модуль радиус-вектора остается постоянным. Следовательно, описывать движение точки можно одним параметром – углом .

Зададим движение точки естественным способом. Ось совпадает с радиусом и проходит через центр окружности, ось направлена в сторону движения точки и перпендикулярна радиусу.

а б

Рис. 2.10

Известно, что длина дуги, радиус окружности и угол связаны между собой:

Введем обозначения:

– круговая скорость, –круговое ускорение.

Вычислим скорость и ускорение точки:

(2.4)

Знак производной определяет направление движения точки:

а при 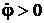, точка движется против часовой стрелки,

b при 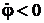, точка движется по часовой стрелки;

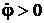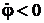c , , или , – точка движется ускоренно;

d , , или , – точка движется замедленно.

Круговое движение точки

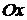Если тело движется, то параметры , и меняются со временем, т. е. являются функциями времени: , , . Поскольку эти параметры независимы, движение тела в плоскости можно разложить на три независимых движения: движение тела вдоль оси – (рис. 2.11, б), движение тела вдоль оси 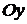– (рис. 2.11, в), вращение твердого тела вокруг полюса А – (рис. 2.11, г). Эти движения принято называть простейшими.

Рис. 2. 11

Уравнения простейших движений твердого тела:

Поступательное движение:

, .

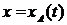При поступательном движении твердого тела траектории скорости и ускорения всех точек тела одинаковы. В этом случае принимаем тело за материальную точку и исследуем поступательное движение тела, как движение материальной точки.

Вращение твердого тела вокруг неподвижной точки А в плоскостиопределяется углом поворота тела (рис. 2.12):

Тогда:

– угловая скорость тела,

– угловое ускорение тела.

При вращении твердого тела его точки движутся по окружности в направлении угловой скорости:

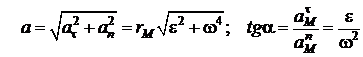Пример. Преобразование поступательного движения тела во вращательное движение другого твердого тела осуществляется при помощи диска, на обод которого намотана нерастяжимая нить (нерастяжимый трос, канат и т. д.) к концу которой прикреплен груз (рис. 2.13).

Рис. 2.1

Запишем уравнения связи. Для этого свяжем перемещение точек соприкосновения нити и обода диска, радиус которого равен

. Пусть тело опустилось на

, тогда все точки нерастяжимой нити прошли путь тоже

, в результате чего диск повернулся на угол

против часовой стрелки.

Имеем . Тогда .

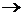
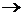
Преобразование вращения одного твердого тела вокруг неподвижной оси во вращение второго твердого тела вокруг другой неподвижной оси осуществляется посредством зубчатого или фрикционного (за счет сил трения) зацепления двух дисков (рис. 2.14, а, б), или при помощи ременной передачи (рис. 2.14, в, г).

При внешнем зацеплении (рис. 2.14, а) и прямой ременной передаче (рис. 2.14, в) направления вращений обоих дисков совпадают; при внутреннем зацеплении (рис. 2.14, б) и скрещивающейся ременной передаче (рис. 2.14, г) направление вращения дисков противоположно.

Рис. 2.14

Примем за ведущее звено диск 1, за ведомое – диск 2. Пусть диск 1 за время повернулся по часовой стрелке на угол , тогда диск 2 повернется против часовой стрелки на угол . Тогда путь , пройденный точками на ободе дисков, находящихся в зацеплении или связанных ременной передачей, одинаков. На этом основании запишем уравнение связи. Напомним, что длина дуги, угол поворота и радиус связаны соотношением . Тогда для всех типов зацепления имеем

. (2.5)

Дифференцируя по времени правые и левые части (2.5), получим

, (2. 5 а)

здесь w₁, w₂ –угловые скорости дисков; r₁, r₂ – радиусы дисков.

Угловые скорости дисков обратно пропорциональны числам зубцов (z_i) или радиусам (r_i), или диаметрам (d_i) дисков.

, (2.5 б)

здесь d₁, d₂ – диаметры дисков; z₁, z₂ – число зубцов каждого диска.

Часто применяется соединение дисков, когда два диска вращаются вокруг одной неподвижной оси. Если при этом они жестко соединены друг с другом, то их угловые скорости равны (на рис. 2.14, в – второй диск).

Содержание контрольных работ для студентов на тему «вычисление кинематических характеристик точек при поступательном и вращательном движениях твердого тела» дано в приложении (контрольная работа 1, задача 2).

Пример 2.3.

Механизм состоит из трех ступенчатых дисков (1–3), находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. На ободах колес расположены точки А, В и С (рис. 2.15).

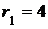Исходные данные: см; см; см; см; см. Уравнение движения , см (за положительное принято движение рейки вниз).

Для момента времени с требуется вычислить характеристики движения: , , ; , , .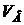

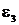Решение

1. Определяем направление движения рейки 4, т. е. всей системы.

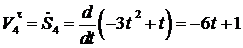(см/с);

для с см/с;

см/с².

Движение рейки 4 (рис. 2.15):

а) поступательное, прямолинейное, т. е. , отсутствует;

б) равноускоренное, т. к. знаки и одинаковы, и ;

в) направлено вверх, т. к. знаки и отрицательны.

Движение остальных тел механизма определяется направлением движения рейки 4 (рис. 2.15).

2. Составляем уравнения связей для всех тел системы, используя точки зацепления между телами и условие, что ремень и нить считаются нерастяжимыми. При используемом в задаче соединении тел знаки параметров сохраняются.

;

Для определения скоростей тел дифференцируем составленные законы движения по времени:

;

; ;

3. Рассчитываем требуемые характеристики движения точек и тел.

Так как точка С и точка зацепления рейки и колеса 3 находятся на одном радиусе этого колеса, то

см/с (рис. 2.15).

Угловое ускорение колеса 3 получаем, дифференцируя по времени выражение угловой скорости

, т.е.

с^-2 (рис. 2.15);

Точка В находится на внешнем ободе колеса 1, тогда

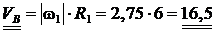см/с (рис. 2.15),

где 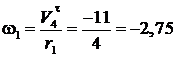с^-1.

Угловое ускорение колеса 1 получаем, дифференцируя по времени выражение угловой скорости

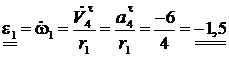с⁻² (рис. 2.15).

Угловая скорость колеса 2:

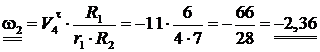с^-1 (рис. 2.15).

Рис. 2.15

Для расчета ускорения точки А, расположенной на внутреннем ободе колеса 2, необходимо рассчитать две составляющие этого ускорения при криволинейном движении этой точки:

, откуда ,

где

(см/с²);

см/с²;

см/с² (рис. 2.15).

Ответ: см/с; см/с²;

см/с; с⁻²;

с⁻¹; с⁻².

Сложное движение точки

Движение точки по отношению к двум или нескольким системам отсчета называется сложным. Движение точки М по отношению к подвижной системе отсчета называется относительным (рис. 2.16). Используются понятия: относительная траектория, относительная скорость ( ) и относительное ускорение ( ).

Рис. 2.16

Движение подвижной системы отсчета по отношению к неподвижной является для точки переносным. Скорость и ускорение точки подвижной системы отсчета, в которой в данный момент времени находится движущаяся точка М, называются переносной скоростью ( ) и переносным ускорением ( ).

Движение точки М по отношению к неподвижной системе отсчета называется сложным или абсолютным. Используются понятия: абсолютная траектория, абсолютная скорость ( ) и абсолютное ускорение ( ).

Теорема. Абсолютная скорость точки равна геометрической сумме ее относительной и переносной скоростей:

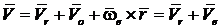здесь: скорость относительного движения;

– скорость переносного движения.

Теорема. Абсолютное ускорение точки равно геометрической сумме трёх ускорений – относительного, переносного и ускорения Кориолиса (или поворотного):

здесь: – ускорение относительного движения;

– переносное ускорение;

– ускорение Кориолиса.

Ускорение Кориолиса ( ) равно удвоенному векторному произведению угловой скорости переносного вращения ( ) на относительную скорость точки ( ):

Модуль ускорения Кориолиса равен

Здесь: угол , угол между вектором относительной скорости 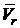и вектором угловой скорости переносного вращения .

Направление ускорения Кориолиса определяется по правилу Жуковского.

Правило Жуковского(рис. 2.17):

1. Следует провести плоскость перпендикулярно оси переносного вращения ( ).

2. Спроецировать вектор относительной скорости на эту плоскость: .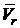

3. Повернуть эту проекцию в этой плоскости на 90⁰по направлению дуговой стрелки переносного вращения .

Содержание контрольных работ для студентов на тему «сложное движение точки» дано в приложении (контрольная работа 1, задача 3).

Пример 2.4. Стержень вращается в плоскости вокруг неподвижного центра в плоскости рисунка с постоянной угловой скоростью . Точка М скользит вдоль стержня со скоростью 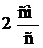. Вычислить абсолютное ускорение точки для момента времени 4 с (рис. 2.18).

Решение. Стержень вращается в плоскости вокруг неподвижного центра с угловой скоростью с^–1. Точка М скользит вдоль стержня со скоростью (рис. 2.18). Абсолютное ускорение точки является векторной суммой трех ускорений: относительного, переносного и ускорения Кориолиса.

здесь: вектор относительного ускорения , т. к.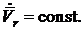

Вектор переносного ускорения

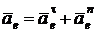где , ,

здесь см.

вектор 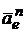направлен пооси .

Ускорение Кориолиса ,

при

Определим направление вектора , используя правило Жуковского. Угол между вектором относительной скорости и равен (вектор ), тогда вектор разворачиваем на по направлению дуговой
стрелки (рис. 2.18).

Вычислим абсолютное ускорение точки :

Тангенс угла (a₁) между и осью равен:

В момент времени ,

Ответ: а_М = 2,83 см/с².

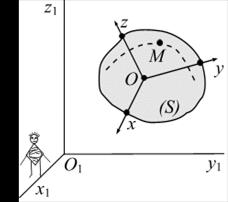
Пример 2.5. Пластина В вращается вокруг неподвижной оси согласно уравнению (рис. 2.19). На пластине по желобу движется точка согласно уравнению

см.

Вычислить абсолютную скорость и абсолютное ускорение точки М в момент времени t = 1 с, если радиус желоба .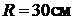

Решение. Будем считать, что в момент времени t = 1 с угол поворота имеет такое значение, при котором тело В располагается в плоскости
(рис. 2.20).

Точка М совершает сложное движение, состоящее из относительного (движение точки по желобу) и переносного (вращение точки вместе с пластиной вокруг оси АС)движений.

Вычислим абсолютную скорость точки :

Относительная скорость . Найдем положение точки М на пластине В через 1с. Для этого вычислим значение дуговой координаты при :

Если обозначить угол, на который опирается дуга ОМ, через a (рис. 2.20), то .

Относительное движение точки задано естественным способом. Приведем оси к точке М на траектории. Относительная скорость точки М при

Вектор относительной скорости лежит в соприкасающейся плоскости относительного движения – плоскость и направлена по касательной к траектории относительного движения – по оси (рис. 2.21, а).

а б

Рис. 2.21

Переносная скорость . В переносном движении точка движется в соприкасающейся плоскости переносного движения, параллельной плоскости , по окружности радиусом (рис. 2.21, б).

Задано уравнение вращения пластины В: , тогда

Переносное движение ускоренное, т. к. >0, >0, дуговые стрелки и направлены в одну сторону (рис. 2.21, б). Приведем оси к точке М.

Вычислим радиус кривизны траектории при переносном движении точки М в момент времени ( ):

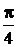=R − = R(1− cosa) = 30(1 – cos( )) = 30(1 – 0,707) = 8,79 см.

Переносная скорость V_е

Вектор переносной скорости направлен по касательной к траектории в точке М – ось 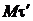(рис. 2.21, б). Направление оси 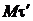согласуется с направлением дуговой стрелки .

Так как в данном случае векторы взаимно перпендикулярны (вектор скорости расположен в плоскости , вектор скорости направлен по оси , т.е. ), то модуль абсолютной скорости точки М:

Вычислим абсолютное ускорение точки М. Абсолютное ускорение точки равно геометрической сумме относительного, переносного и Кориолисова ускорений

Относительное ускорение . Относительное движение точки задано естественным способом – точка движется по окружности радиусом в соприкасающейся плоскости относительного движения . Приведем к точке оси естественного трехгранника (рис 2.22, а). Ось совпадает с направлением , ось перпендикулярна оси и направлена вовнутрь вогнутости траектории по радиусу .

Относительное ускорение равно

Здесь, при t = 1 с:

Точка движется с замедлением, поскольку векторы 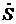>0, <0, вектор и вектор имеют разное направление по оси . Векторы и 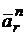направлены по осям и соответственно и лежат в плоскости .

а б

Рис. 2.22

Переносное ускорение . Движение точки в ее переносном движении криволинейное. Точка движется по окружности радиусом в соприкасающейся плоскости переносного движения, параллельной плоскости 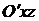. Приведем к точке оси естественного трехгранника (рис 2.22, б). Ось 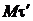совпадает с направлением , ось перпендикулярно оси 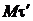и направлена вовнутрь вогнутости, т. е. по радиусу МК.

Переносное ускорение, рис. 2.22, б:

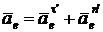Здесь при t = 1 с:

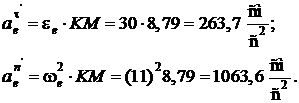
Векторы и направлены по осям 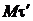и соответственно.

а б

Рис. 2.23

Ускорение Кориолиса . Вектор ускорения Кориолиса

его модуль

Вектор направлен по оси вращения АС. Угол между векторами и равен (b=135^о) (рис. 2.23, а).

Итак,

Направление вектора по правилу Журавского: поворачиваем на 90° по направлению дуговой стрелки 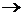вектор направлен параллельно оси (рис. 2.23, б).

Для вычисления модуля абсолютного ускорения используем способ проекций. Спроецируем все составляющие абсолютного ускорения на оси . Имеем (рис 2.22 и рис. 2.23, б):

Модуль абсолютного ускорения (рис. 2.24):

Направление вектора определим геометрически. Совместим с точкой декартову систему координат (рис. 2.24).

Ответ: см/с; см/с².

Рис. 2.24

Дата добавления: 2018-05-12; просмотров: 565; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 3 4 5 6 789 10 11 12 Следующая ⇒

Мы поможем в написании ваших работ!