Траектория, скорость, ускорение материальной точки
Траектория точки. Геометрическое место последовательных положений движущейся точки называется ее траекторией. Если в интервале времени 
траектория - прямая линия, то движение в этом интервале называется прямолинейным, в противном случае движение называется криволинейным.
Скорость точки.Пусть положение движущейся точки М относительно произвольно выбранного неподвижного центра О определяется в момент времени t радиус-вектором 
, который соединяет движущуюся точку М с центром О (рис. 2.1).
За время 
радиус-вектор изменится на 
.
Мгновенная скорость точки 
в момент времени t определяется как предел средней скорости при Dt → 0, т. е.
. (2.1)
Производная по времени от функций обозначается точкой над символом этой функции, а вторая производная – двумя точками.
Вектор скорости приложен в точке М, направлен в сторону ее движения по предельному направлению вектора 
→ 0, т. е. совпадает с касательной к траектории в точке М. Размерность скорости в СИ: 
= длина/время = м/с. Часто скорость выражают в км/ч = 0,28 м/с.
| Скорость– это векторная величина, характеризующая быстроту и направление движения точки |
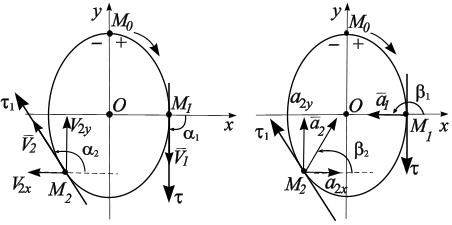
Ускорение точки.Пусть движущаяся точка М в момент времени t имеет скорость (рис. 2.2). В момент времени 
= t + Δt эта точка занимает положение 
, имея скорость 
. Чтобы изобразить приращение скорости 
за время Δt, перенесем вектор скорости 
параллельно самому себе в точку М, тогда 
.
|
|
|
Ускорением точки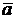 
в момент времени t называют предел, к которому стремится среднее ускорение при Δt → 0, т. е.
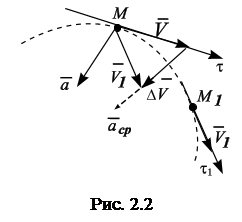
. (2.2)
Вектор ускорения 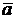всегда направлен внутрь вогнутости под любым углом к касательной к траектории движения (рис. 2.2). Размерность ускорения в СИ: 
= длина/время2 = м/с2.
| Ускорение – это векторная величина, характеризующая быстроту изменения модуля и направления вектора скорости. |
Движение точки на плоскости
Координатный способ задания движения точки. Зададим радиус-вектор в декартовой системе координат Оху:
.
Тогда движение точки можно задать уравнениями
(2.3)
Уравнения (2.3) являются уравнениями движения точки, а также уравнениями траектории точки, заданными параметрически. Уравнение траектории в системе координат 
будет иметь вид функции 
(рис. 2.3). Для получения этой зависимости следует из уравнений (2.3) исключить параметр 
. Уравнение траектории в явном виде будет иметь вид функции .
Скорость и ускорение точки по модулю и направлению вычисляются по формулам:
  ;
 
|
Содержание контрольных работ для студентов на тему «кинематика точки» дано в приложении (контрольная работа 1, задача 1).
|
|
|
Пример 2.1. Движение точки M по плоскости Оху задано уравнениями движения
. (а)
Значения х и у – в метрах. Построить траекторию движущейся точки, вычислить скорость и ускорение точки в моменты времени 
и 
.
Решение. Дляпостроения траектории движущейся точки в декартовой системе координат определим область, в которой движется точка, т. е. область значений 
и 
.[1] Так как 
и 
, получаем:
Выделяем область, ограниченную полученными неравенствами, за эту область точка при движении не выходит (рис. 2.4) Исключим параметр t из уравнений движения (a). Для этого делим первое уравнение на 2, второе – на 4, возводим их в квадрат и складываем между собой:
Учитывая, что 
, получим:
. (б)
Траекторией движущейся точки является эллипс (рис. 2.4). Подставляя в (а) значение 
, находим:
; 
м.
Точка в начальный момент времени занимает положение 
.
Определим направление движения точки. Уравнения движения (а) заданы возрастающей функцией 
и убывающей функцией 
, поэтому при увеличении t координата «х» возрастает, а «у» убывает, следовательно, точка движется по эллипсу по часовой стрелке.
|
|
|
 Рис.2.4
| Определим модуль и направление вектора скорости точки М. Имеем:
 (в)
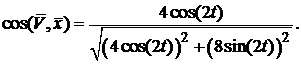Определим модуль и направление вектора ускорения точки М. Имеем:
|
(г)
При из (а) получаем, что точка М имеет координаты х1 = 2,
у1 = 0, т. е. занимает положение (рис. 2.4) М1. Подставляя в (в) и (г) время , получим
Откладываем значение скорости (рис. 2.5, а) и ускорения (рис. 2.5, б) точки М1 на траектории.
При из (а) получаем, координаты точки 
: 
.
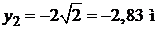Вычислим, используя (в) и (г), модуль и направление векторов скорости и ускорения.
|
| |
| а | б |
| Рис. 2.5 | |
Имеем:
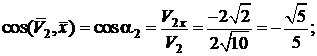
для ускорения
, 
.
Откладываем значение скорости (рис. 2.5, а) и ускорения (рис. 2.5, б) точки на траектории.
Вектор скорости точки совпадает по направлению с касательной к траектории в точках 
и , а вектор ускорения в точках и направлен во внутрь вогнутости траектории (к центру О).
Ответ: V1= 8 м/с, a1= 8 м/с2; V2= 6,3 м/с, a2= 12,6 м/с2.
Естественный способ задания движения точки.
 Рис. 2.6
| При естественном способе задания движения точки задаются (рис. 2.6):
– траектория движения точки;
– начало и направление увеличения дуговой координаты  ;
– уравнение движения точки по траектории, как функция времени:  где S – дуговая координата, отчитываемая от начала движения.
|
Примером естественного способа задания движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано таблицей – расписанием движения поезда.
|
|
|
Движение точки рассматривается в координатах 
. Единичный вектор 
направлен по вектору скорости, единичный вектор 
перпендикулярен вектору , направлен по главной нормали кривой в сторону ее вогнутости (рис. 2.6).
Скорость точки 
направлена по касательной и равна
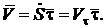
Ускорение 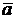точки при естественном способе задания движения раскладывается на два – касательное ускорение 
, и нормальное ускорение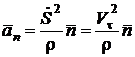 
:
.
Касательное ускорение 
характеризует изменение величины скорости, нормальное 
– изменение направления вектора скорости.
Дата добавления: 2018-05-12; просмотров: 2630; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!