Связь координатного и естественного способов заданий движения точки
|
| Рис. 2.7 |
Известно, что если точка движется в плоскости О 
, элемент дуги 
связан с приращениями координат теоремой Пифагора (рис. 2.7):
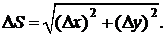
При 
имеем
,
тогда дифференциал дуги 
связан с дифференциалами функций 
и 
(рис.2.7):
,
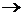
(знак + или - совпадает со знаком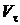 
, так как 
).
Пример 2.2.
Точка движется в плоскости 
. Уравнение движения точки задано координатами 
, 
, где 
и 
выражены в см, 
- в с.
Исходные данные: 
(см); 
(см).
Требуется:
1. Записать уравнение траектории в явном виде: 
(или 
).
2. Построить траекторию.
3. Определить положение точки в начальный момент времени 
и момент времени 
с, направление движения точки по траектории.
4. Вычислить вектор скорости 
и вектор ускорения 
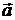точки в начальный ( ) и конечный ( с) моменты времени.
5. Задать движение точки естественным способом (вывести закон 
).
6. Геометрически и аналитически определить нормальную 
и касательную 
составляющие ускорения точки в начальный и конечный моменты времени.
7. Найти радиус кривизны траектории в начальный и конечный моменты времени.
Решение
1. Выводим уравнение траектории в явном виде.
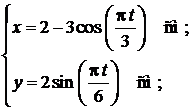
Из первого уравнения системы: 
; из второго уравнения системы: 
. Получаем:
;
;
;
, или 
.
Таким образом, получаем уравнение параболы .
2. Строим траекторию в масштабе 
(рис. 2.8).
Ветви параболы вытянуты вдоль оси . Вершина параболы: 
; 
см 
С (−1;0).
| , см
| ± 1 | ± 2 |
| , см
| 0,5 | 5 |
3. Определяем положение точки в заданные моменты времени.
|
|
|
; 
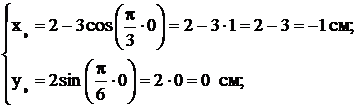М0 (−1; 0);
с; 
М1 (0,5; 1).
Рис. 2.8
Направление движения точки по траектории в промежуток времени от с до 
с определяем по уравнениям движения 
и 
:
· 
– функция убывающая, но она в выражении со знаком
«–», значит, координата возрастает;
· 
– функция возрастающая, значит, координата возрастает.
Таким образом, движение точки по параболе в указанный промежуток времени происходит по часовой стрелке (по верхней ветви параболы) (рис. 2.8).
В целом, точка совершает колебательные движения по построенной параболе в области, указанной пунктиром на графике (рис. 2.8).
4. Вычисляем скорость и ускорение для заданных моментов времени.
Так как движение точки задано координатным способом, то скорость и ускорение 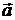определяются по их проекциям на координатные оси (рис. 2.9).
Скорость :
см/с;
см/с;
;
см/с;
см/с;
см/с;
с;
см/с;
см/с;
см/с;
Рис. 2.9
Масштабы: чертежа в 1 см - 0,5 см; скоростей в 1 см - 0,233 см/с; ускорений в 1 см - 0,236 см/с2.
Ускорение :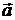
см/с2;
см/с2;
; 
см/с2;
см/с2;
см/с2;
с; 
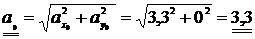см/с2;
см/с2;
см/с2.
Выводим закон движения точки в естественной форме, имеем:
|
|
|
.
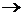
Для промежутка времени от с до с имеем:
;
= 
=
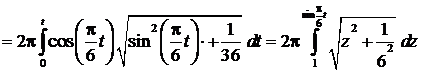, см.
5. Вычисляем нормальное и касательное ускорения.
а) Аналитически:
;
см/с2;
см/с2;
с;
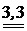см/с2,
= 
см/с2.
Так как 
, 
, движение точки в момент времени с ускоренное.
б) Графическое решение предполагает выполнение геометрического равенства
для соответствующего момента времени (рис. 2.9).
6. Вычисляем радиус кривизны траектории.
Из формулы 
получаем для каждого времени :
; 
см;
с; 
см.
Ответ:
| см | см/с | ||||||||
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
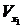
| −1 | 0 | 0,5 | 1 | 0 | 1,05 | 1,05 | 2,7 | 0,9 | 2,8 |
|
| |||||||||
| см/с2 |
| ||||||||
| 
| 
| 
| 
| 
| ||||
| 3,3 | 0 | 3,3 | 1,6 | −0,3 | 1,6 | ||||
|
| |||||||||
| см/с2 | см | ||||||||
|
|
|
|
|
|
| ||||
| граф. | анал. | граф. | анал. | граф. | анал. | граф. | анал. | ||
| 0 | 0 | 3,3 | 3,3 | 1,45 | 1,45 | 0,68 | 0,68 | 0,33 | 11,53 |
Дата добавления: 2018-05-12; просмотров: 569; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!