Лекция 5. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ АВТОМАТИЧЕСКИХ СИСТЕМ.

Понятие устойчивости линейных АСУ.

Оценка устойчивости АСУ является первой задачей при их исследовании. Устойчивость любой физической системы можно сформулировать, как свойство этой системы возвратиться в исходное состояние после того, как она была выведена из него. Например, состояние шара в поле тяготения может быть трёх видов.

Рис. 5.1 а)устойчивое б)неустойчивое в)безразличное

Отклонение системы от установившегося состояния происходит под влиянием внешних воздействий (задающих или возмущающих). Если АСУ описывается линейным дифференциальным уравнением, то общее решение этого неоднородного уравнения складывается из частного решения этого уравнения и общего решения соответствующего однородного, которые в ТАУ называются соответственно вынужденной и переходной составляющими

у(t) = y_B(t) + y_П(t) .

Необходимым и достаточным условием устойчивости линейной АСУ является:

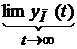= 0 ,

то есть под устойчивостью линейной системы понимают свойство затухания переходного процесса с течением времени. Например, в системе регулирования напряжения при резком увеличении нагрузки напряжение уменьшится, но система будет устойчивой, если с течением времени напряжение примет прежнее значение. Переходная составляющая может быть представлена в виде суммы экспоненциальных членов

у_П(t) = C₁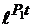+ C₂ + ...+ C_n,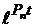

где С₁, С₂, ... С_n - постоянные интегрирования, Р₁...Р_n - корни характеристического уравнения.

a₀pⁿ + a₁pⁿ^-1 + ... + a_n = 0.

Постоянные интегрирования зависят от структуры АСУ и внешних воздействий g(t) и f(t). Они характеризуют лишь количественную сторону переходного процесса и не влияют на устойчивость системы. Устойчивость линейной системы зависит только от вида корней характеристического уравнения.

Линейная система будет устойчивой, если вещественные части всех корней характеристического уравнения будут отрицательными. Это необходимое и достаточное условие устойчивости системы. Если имеется хотя бы один вещественный корень или хотя бы одна пара комплексных сопряженных корней с положительной вещественной частью, то вся система будет неустойчивой.

Различают также три типа границы устойчивости.

Система находится на апериодической границе устойчивости, если в характеристическом уравнении имеется один нулевой корень (на комплексной плоскости он расположен в начале координат), а все остальные корни имеют отрицательные вещественные части (располагаются в левой полуплоскости). Нулевой корень в характеристическом уравнении возможен только при равенстве нулю свободного члена. Такая система является нейтрально устойчивой, в которой у(t) может принимать произвольные значения.

Система находится на колебательной границе устойчивости, если в характеристическом уравнении имеется одна пара чисто мнимых сопряженных корней (вещественные части равны нулю), а все остальные корни имеют отрицательные вещественные части. В системе в этом случае устанавливаются незатухающие гармонические колебания.

Границе устойчивости третьего типа соответствует наличие в характеристическом уравнении бесконечного корня. Например, для характеристического уравнения первого порядка

(с - d)р + а₁ = 0,

корень которого р₁ = а₁/(с - d) будет отрицательным при с < d (система устойчива), положительным при с > d (система неустойчива). А на границе устойчивости с = d, а р₁ = ± ∞.

АСУ, находящиеся на границе устойчивости, неработоспособны, так как малейшее изменение параметров системы может привести к неустойчивости.

Математические условия устойчивости получены при условии, что система описывается линейным дифференциальным уравнением, хотя все реальные АСУ не являются строго линейными. Часто линейные дифференциальные уравнения получаются в результате линеаризации с отбрасыванием нелинейных членов высших порядков. Справедливо ли говорить об устойчивости системы по её линеаризованным уравнениям? При ответе на этот вопрос ссылаются на три теоремы А.М. Ляпунова:

1) Если вещественные части всех корней характеристического уравнения линеаризованной системы отрицательны, то реальная система также устойчива и отброшенные при линеаризации малые нелинейные члены не могут сделать её неустойчивой.

2) Если имеется хотя бы один корень с вещественной положительной частью, то реальная система неустойчива и отброшенные при линеаризации малые нелинейные члены не могут сделать её устойчивой.

3) Если линеаризованная система находится на границе устойчивости, то отброшенные при линеаризации малые нелинейные члены могут сделать реальную систему устойчивой или неустойчивой.

Критерии устойчивости.

Вычисление корней характеристических уравнений просто для уравнений первой и второй степени. Если общие выражения для корней уравнений третьей и четвёртой степени известны, но они громоздки и практически мало удобны. Уравнения более высоких степеней не имеют общих выражений для вычисления корней. Поэтому важное значение приобрели правила, которые позволяют определить устойчивость системы, не вычисляя корней. Эти правила называют критериями устойчивости. Критерии устойчивости можно разбить на две группы: алгебраические и частотные. К алгебраическим критериям относят критерий устойчивости Рауса (Routh) и критерий устойчивости Гурвица (Hurwitz).

Недостатком алгебраических критериев является то, что в случае неустойчивости АСУ они не дают ответа на вопрос, как надо изменить параметры системы, чтобы она стала устойчивой.

Частотные критерии позволяют обеспечить наглядность инженерных расчётов, поэтому иногда их называют графоаналитическими критериями.

Дата добавления: 2018-05-12; просмотров: 372; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 4 5 6 7 8910 11 12 13 Следующая ⇒

Мы поможем в написании ваших работ!