Передаточные функции звеньев.

⇐ ПредыдущаяСтр 6 из 15Следующая ⇒

Для статических звеньев или систем в целом выходная величина у может быть выражена через входную величину х в виде функциональной зависимости у = φ(х). Математическое описание динамической системы осуществляется дифференциальным уравнением. Например, дифференциальное уравнение с постоянными коэффициентами (при f = 0). Введя оператор дифференцирования, получим символическую запись уравнения:

α_Оpⁿy₊...₊α_nу = b_O p^m x + ... + b_mx .

Вынеся у и х за скобки получаем:

у(α_Оpⁿ₊...₊α_n) = х(b_O p^m + ... + b_m) .

Откуда

у = х [ ] .

Выражение в квадратных скобках называется передаточной функцией W(p) звена (системы). С помощью передаточной функции получается самая простая форма записи дифференциального уравнения:

у = W(p) х .

W(p) не имеет физического смысла. Это "функция" от оператора р. Но эта функция позволяет очень просто решать практические задачи и характеризует динамические и статические звенья (системы).

Сложные АСУ и САР можно представить в виде соединения элементарных (типовых) звеньев, которые описываются простейшими передаточными функциями. По виду передаточных функций (или дифференциальных уравнений) и различают типы звеньев АСУ и САР. Основными типами звеньев являются позиционные, дифференцирующие и интегрирующие.

Знание характеристик типовых звеньев столь же необходимо для расчетов систем управления, как знание таблицы умножения в арифметике.

Позиционные звенья

Безынерционное звено описывается уравнением и передаточной функцией:

у = k x ; W(p) = k ,

где k - коэффициент передачи (усиления).

Примером безынерционного звена может служить потенциометр с передаточной функцией W(p) = 1/ R , которая не зависит от р и имеет размерность электрической проводимости.

В этом звене нет переходных процессов, так как выходная величина полностью повторяет процесс изменения входной с коэффициентом k. Безынерционность таких звеньев - это идеализация, так как практически невозможно получить полную безынерционность. Поэтому это звено называют ещё идеальным.

Инерционное (апериодическое звено первого порядка).

Описывается дифференциальным уравнением первого порядка:

Т 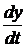+ у = k x ;

где Т - постоянная времени (инерции), k - коэффициент передачи.

В символической записи:

у (Тр + 1) = k x, W(p) = .

Примером апериодического звена можно считать электродвигатель, если х - управляющее напряжение, а у - угловая частота вращения вала. Такое звено моделирует инерционность объектов и применяется для моделирования нагрева, изменения частоты напряжения в сети и т. д.

Инерционные звенья второго порядка.

Описываются дифференциальными уравнениями второго порядка:

(T 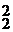p² + T₁p + 1)y = k x ,

Передаточная функция такого звена

W(p) = .

Корни характеристического уравнения:

р_1,2 = - .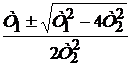

Разложив знаменатель в передаточной функции на сомножители

W(p) = .

Постоянная Т₁, как и в звене первого порядка, моделирует инерцию звена. Чем больше Т₁, тем больше демпфирующее (сглаживающее) действие звена на выходную величину. Постоянная Т₂ характеризует раскачивающее действие звена. От их соотношения зависит вид переходного процесса на выходе.

Если Т₁ ≥ 2 Т₂ , то корни р_1,2 будут вещественными. В этом случае на выходе звена колебаний выходной величины не будет даже при изменении входной величины скачком. Такое звено называют апериодическим звеном второго порядка.

Если Т₁ < 2 Т₂ , то корни р_1,2 будут комплексные. В этом случае получается колебательное звено, на выходе которого будет протекать колебательный процесс. Примером такого звена может быть стрелочный измерительный прибор.

Дата добавления: 2018-05-12; просмотров: 316; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒

Мы поможем в написании ваших работ!