Пропорционально-интегральный закон (ПИ-регулирование)

При комбинированном ПИ регулировании осуществляется пропорциональная и интегральная связь между u(t) и x(t)

u = k_p(x + ) .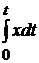

Иногда этот закон называют пропорциональным законом с интегральной коррекцией. При этом законе П-регулирование быстро компенсирует большие по величине возмущения, а И-регулирование осуществляет точную настройку выходной управляемой величины у.

ПИ регуляторы являются астатическими.

Пропорционально-дифференциальный закон (ПД-регулирование).

Алгоритм управления описывается уравнением:

u = k_p(x + ) .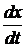

При управлении по производной от ошибки вносится опережение в процесс управления, благодаря которому происходит предварение отклонений выходной величины у от заданного значения. Этот закон позволяет компенсировать инерционность исполнительного устройства.

Пропорционально-интегрально-дифференциальный закон

(ПИД-регулирование)

u = k_p(x +  +  ) .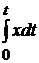

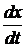При этом законе регулирование будет астатическим, а производная вводится в закон с целью повышения быстродействия системы в переходных процессах.

Позиционное регулирование (релейное)

При этом алгоритме управления задаётся верхний и нижний пределы изменения выходной величины. Примером такой системы могут служить электронагревательные аппараты с терморегулятором.

Виды систем автоматического регулирования.

Все системы автоматического управления и регулирования делятся по различным признакам на следующие классы:

По основным видам уравнений динамики процессов управления:

- линейные системы;

- нелинейные системы.

Каждый из этих основных классов подразделяется на:

- системы с постоянными параметрами (уравнения с постоянными коэффициентами);

- системы с переменными параметрами (уравнения с переменными коэффициентами);

- системы с распределёнными параметрами (уравнения в частных производных);

системы с запаздыванием (уравнения с запаздывающим аргументом).

По характеру передачи сигнала:

- непрерывные;

- дискретные (импульсные и цифровые);

- релейные.

По характеру процессов управления:

- детерминированные (определённые параметры и процессы);

- стохастические (случайные параметры и процессы).

По характеру функционирования:

-обычные;

- адаптивные (самонастраивающиеся, саморегулирующиеся, экстремальные);

- терминальные.

 

Лекция 3. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЭЛЕМЕНТОВ И СИСТЕМ УПРАВЛЕНИЯ.

Использование АСУ позволяет существенно улучшить многие важные параметры технических систем, поэтому для сокращения времени и средств на экспериментальную доводку АСУ желательно иметь возможность судить о её статических и динамических свойствах ещё на стадии проектирования. Для аналитического исследования АС необходимо сделать математическое описание отдельных звеньев и всей системы в целом, то есть выразить существующие связи между переменными и их производными с помощью формул и уравнений.

Математическое описание АСУ и её элементов часто называют математической моделью.

Прежде чем создать математическое описание всей системы, необходимо сделать математическое описание каждого звена в отдельности. Из-за сложности физических связей переменных в реальных устройствах (звеньях) обычно прибегают к упрощенному описанию всех звеньев АС. При этом, в зависимости от условий работы устройства, конкретных целей исследования, выбираются необходимые переменные, учитываются наиболее характерные связи между выбранными переменными и их производными и отбрасываются второстепенные.

В большинстве случаев математическим описанием отдельных устройств являются алгебраические или дифференциальные уравнения. Поэтому сделать описание звена означает составить такое уравнение.

При поэлементном описании АС получают уравнения для отдельных входящих в систему элементов и связей, объединяющих эти элементы в систему. В левые части уравнений включают выходные переменные элементов и их производные по времени, в правые части - входные переменные - воздействия на элементы.

Некоторые переменные будут входными для одного элемента и выходными для другого. Число переменных при таком описании оказывается большим, чем число управляемых переменных, так как оно включает "промежуточные" переменные.

Для получения описания системы в целом желательно исключить все не интересующие исследователя промежуточные переменные и в уравнениях оставить только регулируемые величины и их производные, записываемые в левых частях уравнений и возмущающие и управляющие воздействия на систему в правых частях.

В общем виде статические линейные системы могут быть описаны алгебраическими уравнениями вида:

у = aх + b .

Динамические линейные системы описываются линейными дифференциальными уравнениями, в частности с постоянными коэффициентами.

Для примера представим, что в результате составления уравнения динамики звена получилось линейное дифференциальное уравнение второго порядка:

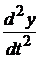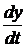α_{О  +} α_{1  +} α₂у = b_{O  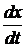+} b₁x .

В ТАУ принято приводить уравнения звена к стандартному виду в символической записи, вводя оператор дифференцирования:

α_Оp²y ₊ α₁py ₊ α₂у = b_Opx ₊ b₁x ,

α₂( p²y + py + y) = b₁( px + x) ,

(T 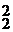p² + T₁p + 1)y = k₁(τ₁p + 1)x ,

где р =  - оператор дифференцирования;

T 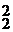 =  , T₁ =  , τ₁ =  - постоянные времени;

k₁ =  - коэффициент усиления звена.

В общем случае при составлении уравнения динамики звена или системы они оказываются нелинейными, описывающимися нелинейным дифференциальным уравнением. Примерами нелинейных звеньев могут быть: электролампа, если рассматривать подаваемое на неё напряжение как входную, а световой поток - как выходную величины; магнитные системы электрических машин и аппаратов, если рассматривать намагничивающий ток как входную, а магнитный поток - как выходную величины.

Если уравнения звеньев нелинейные, то их исследование, решение и даже исключение промежуточных переменных, сильно затрудняется. Поэтому при исследовании нелинейных систем их заменяют приближенной линейной моделью, то есть линеаризуют исходные уравнения, если это допустимо.

Линеаризация уравнений звена

При линеаризации звена нелинейные связи заменяют приближенными линейными, чтобы облегчить процесс исследования регулирования. Естественно, что всякое упрощение при составлении уравнений и их линеаризацией приводит к описанию, неполно отражающему связи переменных, но практически этого во многих случаях оказывается достаточно.

Линеаризация нелинейного дифференциального уравнения основывается на предположении о достаточной малости отклонений всех переменных звена от их установившихся состояний. Это объясняется тем, что замкнутая АС, работающая на принципе отклонений, стремится уменьшить всякие отклонения переменных от требуемых значений.

Если переменные x, f, y в статическом режиме характеризуются установившимися значениями х_О = const; f_O = const; у_О = const, то в динамическом режиме эти переменные можно представить в виде

х(t) = x_O + Δх(t); f(t) = f_O + Δf(t); у(t) = у_О + Δy(t).

То есть для того, чтобы узнать какие значения будут иметь переменные достаточно знать их значения до изменений и знать величину этих изменений. Для этого с достаточной точностью необходимо знать только коэффициенты дифференциального уравнения, связывающего не сами переменные, а только их приращения. Причём если переменные связаны нелинейными уравнениями, то переход к приращениям позволяет перейти к линейным уравнениям, связывающим приращения этих переменных.

Такой переход, безусловно, является приближенным, так как не учтены малые величины высшего порядка, описывает динамический процесс лишь в малой окрестности установившихся значений переменных (x_O, у_О, f_O), а не во всей области их изменений и является линейным лишь относительно отклонений переменных.

Принцип суперпозиции

Существенное упрощение при изучении линейных систем состоит в том, что к ним применим принцип суперпозиции (принцип наложения). В соответствии с этим принципом общая реакция (изменение выходной величины) звена (системы) на несколько входных воздействий равна сумме реакций на каждое воздействие отдельно. При этом математическое описание звена будет одно и то же для всех воздействий.

Принцип суперпозиции позволяет ограничиться изучением реакции звена только на простые возмущения, а реакцию на сложные возмущения изучать как сумму реакций на простые. Чаще всего в качестве простых возмущений используют два вида воздействий: гармоническое колебание и скачок.

---

Дата добавления: 2018-05-12; просмотров: 656; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!