Дифференциальные уравнения замкнутых АС.
Описание замкнутой системы может быть выполнено в виде системы уравнений типа:
αО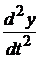 
+ α1 
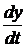+ α2у = bO 
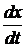+ b1x ,
или в стандартном виде символической записи:
(T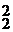 
p2 + T1p + 1)y = k1(τ1p + 1)x .
При описании системы стараются ограничиться уравнениями второго и первого порядков (хотя возможны уравнения и более высокого порядка). Но уравнения второго порядка всегда можно привести к двум уравнениям первого порядка. Представив в аналогичном виде уравнения всех звеньев системы, получим систему уравнений первого порядка, описывающих динамику замкнутой АС.
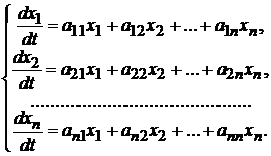
где х1, х2, ... хn - переменные АС, которыми могут быть управляемая величина и её производные, ошибка х и её производные, переменные отдельных звеньев и т.д.
В правых частях необязательно входят все n переменных, поэтому многие коэффициенты будут равны нулю. В некоторые уравнения справа добавятся задающие и возмущающие воздействия.
Запись дифференциальных уравнений в приведенном виде называется нормальной формой или формой Коши.
Частотные характеристики.
К линейным системам применим принцип суперпозиции. В соответствии с ним входной процесс х(t) можно представить в виде суммы процессов, и в частности в виде суммы синусоид (разложение в ряд или интеграл Фурье).
х(t) = хС + 
,
где хС - среднее значение;
хmn и φn амплитуда и фаза соответствующей n-ой гармонической составляющей.
Для оценки входного воздействия на звено достаточно изучить как каждая синусоида (гармоника) воздействует на это звено, а затем результаты воздействий отдельных гармоник сложить, используя принцип суперпозиции. Для оценки воздействия гармонического сигнала на звено используют частотные характеристики звена.
|
|
|
Частотными характеристиками называются зависимости между х(t) и y(t) в виде формул или графиков, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, т. е. вынужденные синусоидальные колебания звена.
Если на вход звена подаётся сигнал в виде синусоиды
х(t) = хm sin ω t
где хm, ω – амплитуда и частота синусоиды.
По окончании переходного процесса на выходе звена устанавливается вынужденный выходной процесс у(t), имеющий ту же частоту, но другую амплитуду Ym и фазу φ:
у(t) = Ym sin(ω t + φ).
Если на вход звена подавать синусоиды одинаковой амплитуды , но разной частоты , то величины А и φ будут на выходе звена разными, то есть они зависят от частоты входного процесса.
Зависимость
А(ω) = Ym(ω)/Хm
и является амплитудно-частотной характеристикой (АЧХ), которая показывает, как изменяется амплитуда выходного сигнала в зависимости от частоты входного.
|
|
|
Фазочастотной характеристикой (ФЧХ) является зависимость фазы выходного сигнала от частоты входного т.е. φ(ω).
АЧХ и ФЧХ можно определить как экспериментальным путем, так и используя дифференциальные или алгебраические уравнения, связывающие входные и выходные величины звена. Но эти методы определения АЧХ и ФЧХ громоздки, особенно если система состоит из множества звеньев.
Для того чтобы по передаточной функции, не решая дифференциального уравнения, найти частотные характеристики необходимо в выражении для передаточной функции звена или системы заменить р на jω, где j = √-1 . То есть получить выражение в комплексной форме
W(jω) = U(ω) + jV(ω) ,
где U(ω) называют вещественной частотной характеристикой, а V(ω) - мнимой. Это же комплексное выражение можно записать в показательной форме:
W(jω) = А(ω) • еjφ(ω).
Все выражение W(jω) называется амплитудо-фазочастотной характеристикой (АФЧХ). Графически АФЧХ характеристика может быть построена в прямоугольных координатах U, V или изображаться на комплексной плоскости в полярных координатах (А, φ), как годограф функции W(jω).
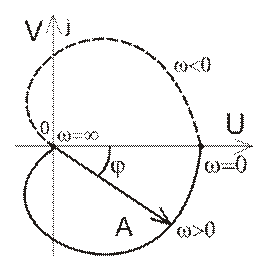
Рис. 4.1. Амплитудо-фазочастотная характеристика.
Для определения величины вектора А необходимо определить модуль выражения W(jω):
|
|
|
А(ω) = W(jω) =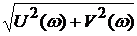 
,
а фаза определяется из выражения
φ(ω) = arctg V(ω)/U(ω) .
Графики АЧХ и ФЧХ также изображаются графически, но на практике, в инженерных расчётах чаще используют логарифмические частотные характеристики. Для построения логарифмической АЧХ (ЛАЧХ) по оси ординат откладывают величину
Lm(ω) = 20 lg A(ω) = 20 lg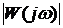 
,
измеряемую в децибелах. По оси абсцисс откладывается частота ω[1/c] в логарифмическом масштабе. Равномерной единицей на оси абсцисс является декада - отрезок, на котором значение частоты увеличивается в десять раз. Ось абсцисс (Lm = 0) соответствует значению А = 1, то есть прохождению сигнала через звено в натуральную величину Ym = Xm . Верхняя полуплоскость ЛАЧХ соответствует значениям А > 1 (усилению амплитуды), а нижняя - значениям А < 1 (ослаблению амплитуды). Начало координат обычно помещают в точке ω = 1 (точка ω = 0 лежит в -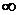 
), хотя может быть и в другой точке (ω =0,1 или ω = 10 и т.д.).
Логарифмическая ФЧХ (ЛФЧХ) имеет ось абсцисс такую же как и у ЛАЧХ, а по оси ординат отсчет φ идет в угловых градусах.
При последовательном соединении звеньев их АЧХ перемножаются, а фазы суммируются.
Частотные характеристики широко используются в электроснабжении при расчете уровней высших гармоник напряжения и тока.
|
|
|
Типовые входные воздействия.
Частотные характеристики позволяют находить решения для стационарного состояния звена или системы. Но иногда возникает необходимость исследования работы системы в переходных режимах.
Переходной процесс в САР вызывается приложением задающего или возмущающего воздействий, а также наличием ненулевых начальных условий.
При нахождении кривой переходного процесса в САР имеется трудность, заключающаяся в том, что в реальных САР воздействия носят случайный характер. Поэтому для описания переходных процессов используют некоторые типовые входные воздействия, чтобы можно было сравнивать работу различных САР в переходных процессах и гарантировать качество переходных процессов САР при всех возможных возмущающих воздействиях.
Обычно используют входные воздействия в виде ступенчатых функций. Для приближенного описания быстро изменяющихся воздействий на входе звена в момент t = tО и в установившемся режиме имеющих постоянное значение используют единичную ступенчатую функцию (единичный скачок или единичная функция Хэвисайда)
х(t - tO) = 1(t - tO) =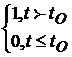 
.
Воздействие такого типа встречается как внезапное включение или отключение электрической нагрузки.
Последовательное включение нескольких нагрузок можно представить как сумму отдельных единичных ступенчатых функций. Плавное непрерывное изменение входного воздействия можно представить как сумму единичных ступенчатых воздействий, разбивая непрерывное входное воздействие на элементарные участки (так называемая решетчатая функция) с шагом Δt → 0.
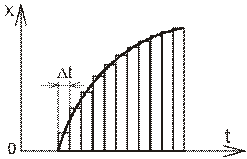
Рис. 4.2. График решётчатой функции.
Кроме единичной ступенчатой функции используют её производную:
δ(t-tO) = 1΄(t-tO) ,
называемую единичной импульсной функцией или дельта-функцией Дирака
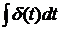= 1.
Её можно трактовать как бесконечно короткий по времени импульс бесконечно большой амплитуды, но с конечной, равной единице площадью. Её можно представить также как прямоугольник площадью 1 сжатый по оси t в прямую бесконечной длины. Воздействия такого типа встречаются в САР в виде кратковременного удара нагрузки (например, при коротком замыкании в электрической сети).
Переходные характеристики.
Для характеристики реакции звена или системы на рассмотренные виды входных воздействий используют следующие переходные характеристики.
Реакция звена (системы) на единичную ступенчатую функцию называется переходной функцией и обозначается h(t - tO)
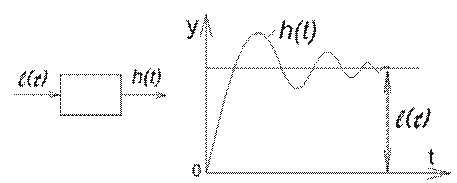
Рис. 4.4. Переходная функция.
Реакция звена (системы) на импульсную функцию называется импульсной переходной функцией или весовой функцией ω(t).
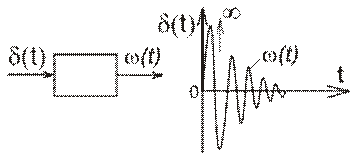
Рис. 4.5. Импульсная переходная функция.
Переходная и импульсная переходная функции находятся путём решения дифференциального уравнения звена (системы) при подаче на вход 1(t) или δ(t). Доказано, что эти характеристики можно найти более простым способом - по передаточной функции этого звена (системы), используя обратное преобразование Лапласа:
h(t) = L-1{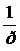 
W(p)},
ω(t) = L-1{W(p)}.
Существуют таблицы обратного преобразования Лапласа для ряда наиболее часто встречающихся выражений.
Например:
L-1{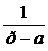 
} = ℓat ,
L-1{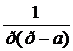 
} = (1-ℓat)/a.
Таким образом, для определения реакции звена (системы) на единичную или дельта-функции достаточно найти выражение для передаточной функции W(p) и осуществить обратное преобразование Лапласа.
Дата добавления: 2018-05-12; просмотров: 382; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!