Нахождение фокуса и директрисы параболы, если известно ее каноническое уравнение.
Общие характеристики эллипса, гиперболы, параболы. Геометрический смысл эксцентриситета.
Теорема. Сечение прямого кругового бесконечного в обе стороны конуса плоскостью, не проходящей через вершину, является или эллипсом, или гиперболой, или параболой. При этом, указанная плоскость может располагаться тремя способами:
1.пересекать одну половину конуса, в этом случае получается эллипс;
2.пересекать обе половины конуса, в этом случае получается гипербола;
3.быть параллельной образующей конуса, в этом случае получается парабола.
Приведение уравнения кривой второго порядка к каноническому виду методом выделения полных квадратов.
Пример. Привести уравнение кривой второго порядка к каноническому виду и построить кривую.
Решение.
Для приведения уравнения кривой второго порядка 
к каноническому виду применяют метод выделения полного квадрата.
Сгруппируем слагаемые, содержащие текущие координаты. Коэффициенты при 
и 
вынесем за скобки: 
Выделим полный квадрат: 
. Отсюда 
. Разделим обе части равенства на 25: 
. Запишем полученное уравнение в каноническом виде: 
.
Выполним параллельный перенос осей координат по формулам 
. При таком преобразовании начало координат переносится в точку 
, уравнение эллипса принимает канонический вид 
.
В нашем примере 
, 
, 
, 
.
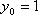Итак, рассматриваемое уравнение определяет эллипс с центром в точке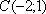 
и полуосями 
и 5.
|
|
|
Рис. 13
Поэтому сходимость или расходимость конкретного ряда является основным вопросом для исследования. Если ряд сходится, то предел общего члена равен 0(необходимое условие сходимости ряда). Обратное, вообще говоря, неверно. Члены ряда могут стремиться к нулю, но ряд при этом может расходиться. Необходимый признак в достаточной форме: если предел не равен 0, то ряд расходится.
Инварианты кривой второго порядка. Определение вида кривой с помощью инвариантов.
Вид кривой зависит от четырёх инвариантов:
*инварианты относительно поворота и сдвига системы координат:
*инвариант относительно поворота системы координат (полуинвариант):
Согласно классификации кривых второго порядка:
I. Если I2 = 0, то данное уравнение (3.1) определяет кривую параболического типа:
I2 = 6 - 2a = 0, следовательно, при a = 3 уравнение определяет кривую параболического типа.
При a = 3 I3 = - a - 95 = -3 - 95 = 98 ¹ 0. Значит, при a = 3 уравнение (3.1) задаёт параболу.
II. Если I2 ¹ 0, то задаваемая кривая является центральной. Следовательно, при a ¹ 3 данное уравнение задаёт центральную кривую.
1.Если I2 > 0, то уравнение задаёт кривую эллиптического типа:
Значит, при a< 3 уравнение (3.1) задаёт кривую эллиптического типа.
|
|
|
a. Если I1 I3 < 0, то уравнение определяет эллипс:
I1 I3 = - (7 - a)(a+95) = a2+88a-665 < 0, при решении получаем a Î (-95 , 7). Следовательно, при a Î (-95 , 3) уравнение (3.1) задаёт эллипс.
b. Если I1 I3 > 0, то уравнение определяет эллипс:
I1 I3 = a2+88a-665 > 0, при решении получаем a Î (-¥, -95). Следовательно, при a Î (-¥ , -95) уравнение (3.1) задаёт мнимый эллипс.
c.Если I3 = 0, то уравнение определяет две мнимые пересекающиеся прямые:
I3 = -a - 95 = 0, при решении получаем a - 95. Следовательно, при a = - 95 уравнение (3.1) задаёт две мнимые пересекающиеся прямые.
2. Если I2 < 0, то уравнение задаёт кривую гиперболического типа:
Значит, при a> 3 уравнение (3.1) задаёт кривую гиперболического типа.
a.Если I3 ¹ 0, то уравнение определяет гиперболу:
I3 = -a - 95 ¹ 0, получаем a ¹ -95. Следовательно, при a Î (3 , +¥) уравнение (3.1) задаёт гиперболу.
Дата добавления: 2018-05-12; просмотров: 452; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!