Разложение вектора по базису.
Определение линейного пространства
Множество L называется линейным или векторным пространством, если для всех элементов (векторов) этого множества определены операции сложения и умножения на число и справедливо:
1. Каждой паре элементов x и y из L отвечает элемент x + y из L, называемый суммой x и y, причём:
x + y = y + x − сложение коммутативно;
x + (y + z) = (x + y) + z − сложение ассоциативно;
x + 0 = x − существует единственный нулевой элемент 0 ( x + 0 = x для любого x из L);
x + (− x) = 0 − для каждого элемента x из L существует единственный противоположный элемент −x( x + (−x) = 0 для любого x из L).
2. Каждой паре x и α, где α − число, а x элемент из L, отвечает элемент α·x, наываемый произведением α и x, причём:
α·(β·x) = (α·β)·x − умножнение на число ассоциативно: ;
1·x = x − для любого элемента x из L.
3. Операции сложения и умножения на число связаны соотношениями:
α·(x + y) = α·x + α·y − умножнение на число дистрибутивно относительно сложения элементов;
(α + β)·x = α·x + β·x − умножнение на вектор дистрибутивно относительно сложения чисел.
Базис линейного пространства.
Определение ->Базисом линейного пространства Lназывается такая конечная упорядоченная линейно независимая система векторов, что любой вектор пространства L является линейной комбинацией этих векторов.В отличие от трехмерного пространства векторов, в некоторых линейных пространствах базис не существует.
|
|
|
Теорема ->В линейном пространстве любые два базиса содержат одинаковое число векторов.
Определение ->Линейное пространство L , в котором существует базис, состоящий из n векторов, называется n -мерным линейным или векторным пространством. Число n называется размерностью пространства и обозначается dimL . Линейное пространство, в котором не существует базис, называется бесконечномерным.Примером бесконечномерного пространства является пространство всех многочленов с вещественными коэффициентами.
Основные примеры линейных пространств и стандартные базисы в них.
Кроме выше описанного детального примера линейного векторного пространства можно привести еще массу примеров множеств, которые также являются линейными пространствами. К таким множествам относится
Множество всех полиномов фиксированной степени. Причем суммой двух многочленов будет являться многочлен с коэффициентами, равными суммам коэффициентов слагаемых, а произведением многочлена на число будет многочлен с коэффициентами исходного многочлена, умноженными на это число.
Матрицы порядка n. Суммой двух матриц является матрица, составленная из сумм элементов исходных матриц, а произведением матрицы на число будет матрица из произведений элементов исходной матрицы на это число. Нулевым элементом при этом будет матрица состоящая из одних нулей. Легко проверяется по аналогии с векторами на плоскости, что все аксиомы линейного пространства для множества квадратных матриц фиксированной размерности выполнены.
|
|
|
Элементы линейного пространства также по аналогии называют векторами, однако они могут и не быть обычными векторами плоскости или прямой, или трехмерного пространства. Векторами мы будем называть и матрицы и многочлены и все остальные математические объекты, которые удовлетворяют аксиомам линейного пространства.
Линейная зависимость и независимость элементов линейного пространства.
Линейная зависимость и независимость векторов. Базис.
Определение. Векторы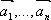 
называются линейно зависимыми, если существует такая линейная комбинация 
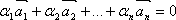, при не равных нулю одновременно ai , т.е. 
.
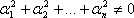Если же только при ai = 0 выполняется 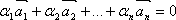, то векторы называются линейно независимыми.
Свойство 1. Если среди векторов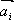 
есть нулевой вектор, то эти векторы линейно зависимы.
Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
|
|
|
Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.
Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.
Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.
Свойство 6. Любые 4 вектора линейно зависимы.
Утверждение. Система векторов линейного пространства V является линейно зависимой тогда и только тогда, когда один из векторов является линейной комбинацией векторов этой системы.
Определение. Базисом линейного пространства V называется такая конечная упорядоченная линейно независимая система n векторов, что любой вектор пространства V является линейной комбинацией этих векторов (т.е. любая система из n+1 векторов является линейно зависимой).
Разложение вектора по базису.
Линейной комбинацией векторов a1, ..., an с коэффициентами x1, ..., xn называется вектор
x1a1 + ... + xnan.
Чтобы разложить, вектор b по базисным векторам a1, ..., an, необходимо найти коэффициенты x1, ..., xn, при которых линейная комбинация векторов a1, ..., an равна вектору b,
x1a1 + ... + xnan = b,
при этом коэффициенты x1, ..., xn, называются координатами вектора b в базисе a1, ..., an.
Дата добавления: 2018-05-12; просмотров: 485; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!