Приведение квадратичной формы к диагональному виду методом элементарных преобразований.
Приведение квадратичной формы к диагональному виду методом Лагранжа.
Канонический вид квадратичной формы. Положительный и отрицательный индексы инерции квадратичной формы. Ранг квадратичной формы.
Квадратичная форма называется канонической, если все 
т. е.
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
1. Ортогональное преобразование пространства 
:
где 
- собственные значения матрицы A.
2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если 
Затем подобную процедуру проделывают с квадратичной формой 
и т. д. Если в квадратичной форме все 
но есть 
то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например, 
то полагаем 
3. Метод Якоби (в случае, когда все главные миноры 
квадратичной формы отличны от нуля):
Пусть k(x) — квадратичная форма, заданная в пространстве арифметических векторов Rn.
В пространстве Rn существует канонический базис квадратичной формы, базис, в котором матрица квадратичной формы является диагональной.
В этом базисе квадратичная форма имеет канонический вид
k(x) = λ1x12 + λ2x22 + ... + λnxn2.
Числа λ1, λ2, ... , λn — канонические коэффициенты квадратичной формы.
Закон инерции квадратичных форм гласит: число положительных, отрицательных и нулевых канонических коэфициентов квадратичной формы не зависит от преобразования, с помощью которого квадатичная форма приводится к каноническому виду.
|
|
|
Число положительных канонических коэфициентов квадратичной формы называется положительным индексом инерции квадратичной формы. Число отрицательных канонических коэфициентов квадратичной формы называется отрицательным индексом инерции квадратичной формы. Разность междуположительным и отрицательным индексами квадратичной формы называется сигнатурой квадратичной формы. Число ненулевых канонических коэффициентов называется рангом квадратичной формы.
Положительно определенные квадратичной формы. Критерий Сильвестра.
Определение эллипса. Фокусы эллипса.
Определение. Эллипс - это геометрическая фигура, которая ограничена кривой, заданной уравнением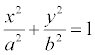 
.
Чертёж элипса
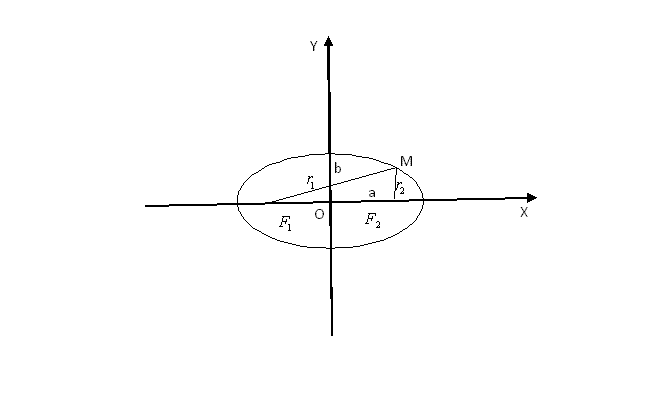
F1 , F2 – фокусы . F1 = ( c ; 0); F 2 (- c ; 0)
с – половина расстояния между фокусами; a – большая полуось; b – малая полуось.
Теорема. Фокусное расстояние и полуоси связаны соотношением:
a2 = b 2 + c 2.
Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r1 + r2 = 2* 
(по теореме Пифагора). В случае, если точка М находится на пересечении его с горизонтальной осью, r1 + r 2 = a – c + a + c. Т.к. по определению сумма r1 + r 2 – постоянная величина, то , приравнивая, получаем:
|
|
|
a 2 = b 2 + c 2
r1 + r2 = 2 a .
Дата добавления: 2018-05-12; просмотров: 2897; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!