Замена базиса в линейном пространстве. Изменение координат вектора при замене базиса.
Линейные подпространства. Сумма и пересечение подпространств. Прямаясуммаподпространств.
Подпространство
Алгебраическое определение: Линейное подпространство или векторное подпространство ― непустое подмножество 
линейного пространства 
такое, что само является линейным пространством по отношению к определенным в действиям сложения и умножения на скаляр. Множество всех подпространств обычно обозначают как 
. Чтобы подмножество было подпространством, необходимо и достаточно, чтобы
1. 
;
2. для всякого вектора 
, вектор 
также принадлежал , при любом 
;
3. для всяких векторов 
, вектор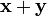 
также принадлежал 
.
Последние два утверждения эквивалентны следующему:
для всяких векторов , вектор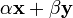 
также принадлежал для любых 
.
В частности, пространство, состоящее из одного элемента 
, является подпространством любого пространства; любое пространство является само себе подпространством. Подпространства, не совпадающие с этими двумя, называют собственными или нетривиальными.
Сумма и пересечение подпространств.
Пусть L1..Lk – линейные подпространства пространства V. Суммой подпространств L1..Lk называется множество всевозможных векторов x, представимых в виде x = x1 + … + xk, где xi из Li для любых i от 1 до k. Обозначается как L1 + L2 +.. + Lk
Представление вектора в виде такой суммы называется разложением вектора x по подпространствам L1.. Lk
Пересечением подпространств L1..Lk называется множество, в котором содержаться только те вектора, которые содержатся в каждом из подпространств L1..Lk
|
|
|
Пересечение пустым не бывает, как минимум это нулевой вектор.
Теорема. Сумма и пересечение подпространств линейного пространства V также является подпространством V.
Доказательство следует из определения подпространства.
Теорема. Сумма линейных подпространств есть линейная оболочка совокупности базисов слагаемых подпространств.
Доказательство – просто проверяем двустороннее вложение.
Следствие. Размерность суммы подпространств равна рангу мовокупности базисов слагаемых подпространств.
Теорема. Для любых двух подпространств выполняется равенство dim(L1+L2) = dimL1 + dim L2 – dim(L1^L2)
Доказательство.
Если пересечение ненулевое, то смотрим его базис – f1..fn – так как пересечение является подпространством каждого из исходных подпространств, этот базис можно дополнить до базиса каждого из подпространств. Дополним, получим два базиса. В каждом из них будет n векторов из базиса пересечения. А если дополнить до базиса совокупности сразу, получим n векторов из базиса пересечения и еще m и s дополняющих векторов до базиса первого и второго подпространства. То есть, m+s+n = m+n + s +n – s – верно, доказано.
|
|
|
Прямая сумма пространств
Пусть L -лин пространство и в нем есть 2 подпространства M и N
L есть прямая сумма M и N, если выполняются 2 условия
1)М пересек N ={0}
2)для всех x прин L сущ x1 прин M и сущ x2 прин N:x=x1+x2
Теорема: Пусть L=прямое пересечение M и N, тогда
1)x=x1+x2 x1 и x2 определяются единственным образом
2)Если e1,...,ek базис в M, а f1,...,fr базис в N, то e1,...,ek,f1,...,fr базис в L
Не всегда
3)dim L=dimM+dimN (следствие 2)
1)х=x1+x2=x1'+x2'
x1,x1' прин M
x2,x2' прин N
x1-x1'=x2'-x2 Так как между ними рав-во, то они принадлежат обоим множествам => x1=x1' x2=x2'
2)e1,...,ek базис в M, а f1,...,fr базис в N
1 свойство - линнез
2 свойсвто - можно разложить по базису
2-ое
x=x1+x2=альфа1e1+...+альфаkek+бета1f1+...+бетаrfr
люб вектор можно разложить по базису
1-ое
Пусть альфа1e1+...+альфаkek+мю1f1+...+мюrfr=0, докажем что все коэфф=0
альфа1e1+...+альфаkek=-мю1f1-...-мюrfr
прин M прин N
обе суммы равны 0, но т.к. это базис они линнезав=> все коэфф=0
Дата добавления: 2018-05-12; просмотров: 446; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!