Линейная функция. Определение, примеры.
Линейная функция, функция вида у = kx + b. Основное свойство Л. ф.: приращение функции пропорционально приращению аргумента. Графически Л. ф. изображается прямой линией. При равных масштабах на осях коэффициент k; (угловой коэффициент) равен тангенсу угла, образованного прямой с осью Ox( k = tg j, см. рис.), а b — отрезку, отсекаемому прямой на оси Оу. При b = 0 Л. ф. называется однородной; её график изображает пропорциональную зависимость: у = kx. Л. ф. широко применяется в физике и технике для представления (нередко — приближённо) зависимостей между различными величинами. Рассматривают также Л. ф. многих переменных; однородные Л. ф. многих переменных называют линейными формами. Если и аргумент и функция суть векторы, то однородными Л. ф. являются линейные преобразования.
Пример.

Линейная функция.
Билинейная функция. Определение, примеры.
Билинейная функция - это функция двух аргументов t и u, которая при фиксированном значении t линейна по u и наоборот. Билинейный сплайн является двухмерным обобщением одномерного линейного сплайна и имеет те же достоинства и недостатки. Он составляется из билинейных функций, определенных на каждой ячейке сетки так, что в узлах сетки они принимают предписанные значения. Этот способ интерполяции хорош своей простотой и быстродействием. Основной недостаток - разрывность производной интерполирующей функции на границах ячеек сетки. Также можно отметить сравнительно невысокую точность такой интерполяционной схемы.
Матрица билинейной функции. Нахождение значения билинейной функции, если известна ее матрица.
Изменение матрицы билинейной функции и квадратичной формы при переходе к новому базису.
Квадратичные формы. Связь с билинейными функциями. Матрица квадратичной формы.
Квадратичная форма, форма 2-й степени от n переменных x1, x2,..., xn, т. е. многочлен от этих переменных, каждый член которого содержит либо квадрат одного из переменных, либо произведение двух различных переменных. Общий вид К. ф. при n = 2:
 ,
,
при n = 3:
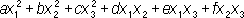 ,
,
где a, b,..., f — какие-либо числа. Произвольная К. ф. записывается так:
 ;
;
причём считают, что aij = aji. К. ф. от 2, 3 и 4 переменных непосредственно связаны с теорией линий (на плоскости) и поверхностей (в пространстве) 2-го порядка: в декартовых координатах уравнение линии и поверхности 2-го порядка, отнесённых к центру, имеет вид А (х) = 1, т. е. его левая часть является К. ф.; в однородных координатах левая часть любого уравнения линии и поверхности 2-го порядка является К.ф. При замене переменных x1, x2,..., xn др. переменными y1, y2,..., yn, являющимися линейными комбинациями старых переменных, К. ф. переходит в другую К. ф. Путём соответствующего выбора новых переменных (невырожденного линейного преобразования) можно привести К. ф. к виду суммы квадратов переменных, умноженных на некоторые числа. При этом ни число квадратов (ранг К. ф.), ни разность между числом положительных и числом отрицательных коэффициентов при квадратах (сигнатура К. ф.) не зависят от способа приведения К. ф. к сумме квадратов (закон инерции). Указанное приведение можно осуществить даже специальными (т. н. ортогональными) преобразованиями. Геометрически в этом случае такое преобразование соответствует приведению линии или поверхности 2-го порядка к главным осям.
При рассмотрении комплексных переменных изучаются К. ф. вида

где — число, комплексно сопряженное с xj. Если, кроме того, такая К. ф. принимает только действительные значения (это будет, когда ( ), то её называют эрмитовой. Для эрмитовых форм справедливы основные факты, относящиеся кдействительным К. ф.: возможность приведения к сумме квадратов, инвариантность ранга, закон инерции.
Дата добавления: 2018-05-12; просмотров: 457; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
