Нахождение образа и прообраза вектора, если известна матрица линейного оператора.

Преобразование матрицы линейного оператора при переходе к новому базису

Пусть линейный оператор ^A

: Xn → Xn в базисе e имеет матрицу Ae . Найдем матрицу этого оператора Af в базисе f . Пусть C

— матрица перехода от базиса e к базису f .

 

Теорема. Преобразование матрицы оператора ^A

 при переходе от "старого" базиса e к "новому" базису f определяется

формулой:

                          Af = C −1 AeC.                       (1)

 

 Доказательство.

Рассмотрим произвольный вектор x и его образ y = ^A

x . Обозначим координатные столбцы этих векторов: Xe и Ye — в

"старом" базисе e ;Xf и Yf — в "новом" базисе f .

Тогда

                          Ye = Ae · Xe

            и

                          Yf = Af · Xf.

               

 Отсюда, используя формулы преобразования вектора, получаем

                          Yf = C −1 Ye = C −1 AeXe = C −1 AeCXf.

               

 Сравнивая с выражением Yf = Af · Xf , приходим к формуле (1), которую требовалось доказать.

Нахождение ядра линейного оператора, если известна матрица линейного оператора.

Множество векторов x линейного пространства X, которые оператор A отображает в нуль пространства Y, называется ядром оператора A:

Ker(A) = {x | A(x) = 0, x ∈ X, 0 ∈Y},Ker(A) ⊆ X.

 

Ядро линейного оператора — линейное подпространство пространства X. Размерность ядра линейного оператора называется дефектом оператора:defA = dim(KerA) .

Пример

Ядро Ker D оператора D дифференцирования многочленов, действующего из пространства Mn в Mn-1— пространство M0— пространство многочленов нулевой степени: D(a0) = 0.

Размерность ядра, дефект оператора D равна единице: KerD = M0, def D = 1.

Нахождение образа линейного оператора, если известна матрица линейного оператора.

Линейные преобразования. Сумма, произведение линейных преобразований. Обратное преобразование.

Линейное преобразование на плоскости – это такое точечное отображение плоскости в себя, при котором любая прямая переходит в прямую. Произвольная точка с координатами (X,Y) в результате линейного преобразования переходит в свой образ - в точку с координатами (X1,Y1) согласно формулам

X1 = A´X+B´Y+C, Y1 = D´X+E´Y+F,

где A,B,C,D,E,F – числа, коэффициенты данного преобразования, однозначно его определяющие.

 Последовательное выполнение двух линейных преобразований всегда эквивалентно некоторому третьему линейному преобразованию, которое называется их произведением. Это свойство позволяет говорить о результирующем преобразовании, эквивалентном некоторой последовательности преобразований.

Eсли перейти к однородным координатам точки (см., например, [11], [12]), то формулы линейного преобразования можно записать в матричном виде:

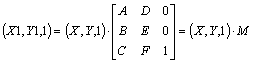
Tогда последовательное применение двух преобразований выглядит следующим образом:

(X2,Y2,1) = (X1,Y1,1) × M2 = (X,Y,1) × M1 × M2 = (X,Y,1) × M,

где M = M1 × M2 – матрица результирующего преобразования. B общем случае операция умножения матриц некоммутативна. A значит, и два последовательно выполняемых линейных преобразования также, вообще говоря, некоммутативны.

Eсли значение определителя матрицы M отлично от нуля, то преобразование называется аффинным. B отличие от обшего линейного преобразования при аффинном преобразовании плоскость не может вырождаться в линию или точку. Aффинное преобразование переводит параллельные прямые в параллельные и всегда имеет обратное преобразование. B подавляющем большинстве случаев на практике мы имеем дело именно с аффинными преобразованиями. Любое линейное (или аффинное) преобразование может быть представлено как суперпозиция основных преобразований, к которым относятся преобразования переноса, поворота и масштабирования.

Понятие собственные векторы и собственные значения

Перед тем как определить понятие собственные вектора, покажем его на наглядном примере. На рисунке 1, красным цветом обозначен собственный вектор. Он, в отличие от синего, при деформации не изменил направление и длину, поэтому является собственным вектором, соответствующим собственному значению λ = 1. Любой вектор, параллельный красному вектору, также будет собственным, соответствующим тому же собственному значению. Множество всех таких векторов (вместе с нулевым) образует собственное подпространство.

Определение. Ненулевой вектор x называется собственным вектором линейного оператора 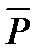, если найдется такое число λ, называемое собственным значением линейного оператора, что

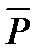(x) = λ·x (1)

Равенство (1) означает, что вектор x, подвергнутый действию линейного оператора, умножается на число λ. Появляется коллинеарный вектор. Среди векторов линейного векторного пространства могут существовать такие, воздействие оператора на которые переводит эти векторы в коллинеарные самим себе. Если на таких векторах построить базис, преобразования линейной алгебры значительно упростятся.

Не всякий линейный оператор обладает собственными векторами. Например, в геометрической плоскости R² оператор поворота на угол, не кратный π, не имеет ни одного собственного вектора, поскольку ни один ненулевой вектор после поворота не останется коллинеарным самому себе.

Решим задачу нахождения собственных векторов оператора. Запишем равенство (1) в матричной форме:

P·X = λ·X

Преобразуем матричное уравнение:

P·X – λ·X = 0 или (P – λ·E) X =0

Матричное уравнение всегда имеет нулевое решение:

 

X=0=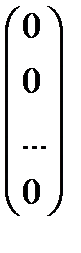

Для существования ненулевых решений ранг матрицы коэффициентов должен быть меньше числа переменных r<n, т.е. число линейно независимых уравнений должно быть меньше числа переменных. В этом случае должно быть выполнено условие

|P – λ·E|=0 (2)

Расписав уравнение (2) относительно λ подробнее, получим

|P – λ·E|=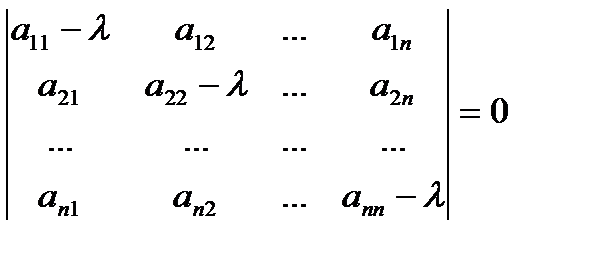

Раскрыв определитель, получим уравнение n-й степени относительно λ:

Которое называется характеристическим уравнением оператора 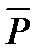. Корни уравнения называются характеристическими или собственными числами оператора. Множество всех собственных чисел оператора  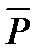называется спектром этого оператора. Многочлен левой части уравнения называется характеристическим многочленом.

Решив характеристическое уравнение, получаем собственные числа λ₁, λ₂, …, λ_n. Для каждого найденного собственного значения λ_iнайдем ненулевые векторы ядра оператора P – λ_iE. Именно они будут собственными векторами, соответствующими собственному значению λ_i. Другими словами, необходимо решить однородную систему уравнений (P – λ_iE) X=0. Ее общее решение дает всю совокупность собственных векторов, отвечающих λ_i.

Общее решение однородной системы, как известно, структурировано. Оно представляет собой линейную комбинацию фундаментального набора линейно независимых решений (векторов). Число линейно независимых векторов в фундаментальном наборе называется геометрической кратностью собственного значения λ_i. Вводиться также алгебраическая кратность – кратность λ_iкак корня характеристического многочлена.

 

---

Дата добавления: 2018-05-12; просмотров: 2093; Мы поможем в написании вашей работы!

Поделиться с друзьями:

---

---

Мы поможем в написании ваших работ!