Угол (определение). Развернутый угол. Внутренняя и внешняя область угла.
Основное свойство откладывания углов.
Угол — это геометрическая фигура, состоящая из двух различныхлучей, выходящих из однойточки.
Лучи называются сторонами угла, а их общее начало — вершиной угла.
Развернутый угол — этоугол, стороны которого лежат на одной прямой.Градусная мера развёрнутого угла равна 180º.Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами. Угол разделяет плоскость на две части, каждая из которых также называется углом, то может возникнуть неоднозначность в том, какой именно из углов рассматривается. Чтобы наглядно показать, о каком именно угле идёт речь, на чертеже обычно делается какое-нибудь специальное обозначение.
Тот из углов, который рассматривается, на чертеже обычно отмечают дугой, проведённой от одной стороны угла до другой:

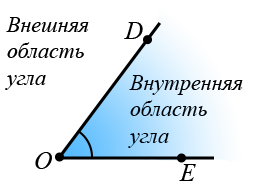
| Часть плоскости, расположенная между сторонами рассматриваемого угла называется внутренней областью угла. Часть плоскости не принадлежащая рассматриваемому углу называется внешней областью угла: |
От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.
Теорема о существовании и единственности перпендикуляра к прямой.
Теорема.
Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.
Доказательство
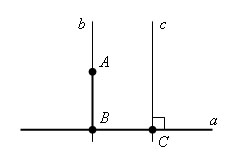
Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.

Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.
3. Задача по теме "Сумма углов треугольника ".
Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.
Дата добавления: 2018-05-12; просмотров: 2657; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
