Построение угла, равному данному.

Отложить от данного луча угол, равный данному.

Решение. Данный угол с вершиной А и луч ОМ

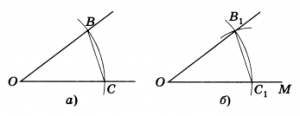
Проведем произвольную окружность с центром в вершине О данного угла. Пусть В и С — точки пересечения окружности со сторонами угла (рис а). Радиусом ОВ проведем окружность с центром в точке О — начальной точке данного луча (рис. б). Точку пересечения этой окружности с данным лучом обозначим С₁. Опишем окружность с центром С₁ и радиусом ВС. Точка В₁ пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ОBC = Δ ОВ₁С₁(третий признак равенства треугольников).

2. Задача по теме "Внутренние и внешние углы треугольника ".

Один из внешних углов прямоугольного треугольника равен 130º. Найдите острые углы треугольника

Билет № 19

Отрезок (определение). Длина отрезка. Основное свойство измерения отрезков.

Отрезок - это часть прямой, которая ограничена двумя точками, т.е. она имеет начало и конец, а значит можно измерить её длину

Расстоянием между двумя точками называется длина отрезка .

1.Каждый отрезок имеет определенную длину, большую нуля.

2.Длина отрезка равняется сумме длин частей, на которые он разбивается любой своей внутренней точкой.

3.При этом, если точки A и B совпадают, будем считать, что расстояние между ними равно нулю.

4.Два отрезка называются равными, если равны их длины.

Теорема о соотношении между сторонами и углами треугольника.

Теорема

В треугольнике:

1) против большей стороны лежит больший угол;

Против большего угла лежит большая сторона.

1) Дано: ∆ ABC, AC>AB.

Доказать: ∠B>∠C.

Доказательство:

Отложим на стороне AC отрезок AK: AK=AB.

Так как AC>AB, то точка K лежит между точками A и C. Следовательно, ∠ABC=∠ABK+∠KBC, то есть ∠ABC>∠ABK.

Так как AK=AB, то треугольник ABK — равнобедренный с основанием BK.

Значит, у него углы при основании равны: ∠ABK=∠AKB.

Для треугольника BCK ∠AKB — внешний.

Поэтому ∠AKB=∠KBC+∠C, а значит, ∠AKB>∠C.

Имеем:

2) Дано: ∆ ABC,

∠B>∠C.

Доказать: AC>AB.

Доказательство:

(методом от противного).Предположим, что неравенство AC>AB — неверное. Тогда либо AC=AB, либо AC<AB.Если AC=AB, то треугольник ABC — равнобедренный с основанием BC и у него углы при основании равны: ∠B=∠C, что противоречит условию.По доказанному в пункте 1), против большей стороны лежит больший угол. Поэтому, если AC<AB, то ∠B<∠C. Снова пришли к противоречию.Значит, выдвинутое нами предположение неверно. Следовательно, AC>AB.

Что и требовалось доказать.

3. Задача по теме "Виды треугольников ".

Периметр равностороннего треугольника DEK равен 18 см. Найдите стороны треугольника DEK .

Билет № 20

Дата добавления: 2018-05-12; просмотров: 1310; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 1 2 3 4 5 6 789 Следующая ⇒

Мы поможем в написании ваших работ!