Внешний угол треугольника (определение). Теорема о внешнем угле треугольника.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
Доказательство.
Пусть ABC – данный треугольник. По теореме о сумме углов в треугольнике
| ∠ ABС + ∠ BCA + ∠ CAB = 180 º. Отсюда следует ∠ ABС + ∠ CAB = 180 º - ∠ BCA = ∠ BCD Теорема доказана. |
3. Задача по теме "Признаки равенства прямоугольных треугольников".
У треугольников ABC и DEK: 
, AC=DK, AB=DE. Докажите, что 
.
Билет № 10
1. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников (без доказательства).
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть составляет 90 градусов)
Признак равенства прямоугольных треугольниковпо двум катетам
Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
Признак равенства прямоугольных треугольниковпо катету и гипотенузе
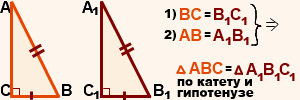
Если катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Признак равенствапо гипотенузе и острому углу
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
|
|
|
Признак равенства прямоугольных треугольниковпо катету и острому углу
Если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Параллельные прямые (определение). Признаки параллельности двух прямых (доказательство одного из них).
Две прямые a и b на плоскости, которые не пересекаются, называются параллельными и обозначаются a∥b.
Признак 1: Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Доказательство:
Через точку К - середину отрезка секущей - проведем перпендикуляр к прямой b - КН, продлим его до пересечения с прямой а.
АК = КВ, так как К середина АВ,
углы при вершине К равны как вертикальные,
∠КВН = ∠КАН' по условию, ⇒
ΔВКН = ΔАКН' по стороне и двум прилежащим к ней углам.
Значит ∠АН'К = ∠ВНК = 90°.
Обе прямые а и b перпендикулярны третьей прямой НН', значит они параллельны.
Признак 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Доказательство:
∠1 = ∠2 по условию (соответственные углы)
|
|
|
∠3 = ∠1 как вертикальные, ⇒
∠2 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому признаку.
Признак 3: Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Доказательство:
∠1 + ∠2 = 180° по условию (односторонние углы),
∠2 + ∠3 = 180° так как эти углы смежные,
значит ∠1 = ∠3, а это накрест лежащие углы, значит прямые параллельны по первому признаку.
3. Задача по теме " Угол. Измерение углов".
Известно, что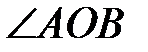 
=90º. Луч OD делит угол AOB на два угла: 
и 
. Найдите 
, если угол AOD в два раза меньше угла DOB.
Билет № 11
Дата добавления: 2018-05-12; просмотров: 4377; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!