Взаимное расположение двух прямых. Основное свойство параллельных прямых.

⇐ ПредыдущаяСтр 2 из 9Следующая ⇒

1)прямые пересекаются (т. е. имеют одну общую точку), 2) прямые параллельны и не совпадают, 3) прямые совпадают( множ-во общих точек)

Через точку не лежащую на прямой, можно провести прямую параллельную данной, причем только одну.

Вертикальные углы (определение). Свойства вертикальных углов.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Вертикальные углы равны

Дано: – 1 и – 2 – вертикальные углы.

Доказать: – 1 = – 2.

Доказательство. – 3 является смежным и с – 1, и с – 2. Сумма смежных углов равна 180°, поэтому – 1 + – 3 = 180о , – 2 + – 3 = 180о . Отсюда получаем, что – 1 = 180о –– 3, – 2 = 180о – – 3. Пра- вые части равенств равны, значит, равны и левые. Следовательно, – 1 = – 2. Итак, вертикальные углы равны

3. Задача по теме " Соотношения между сторонами и углами

треугольника".

В треугольнике ABC AB=4 см, AC=6 см,BC=5 см. Какой угол треугольника наименьший, а какой наибольший?

Билет №6

Полуплоскость. Луч (определение). Основное свойство расположения точек относительно прямой на плоскости.

Любая прямая на плоскости разделяет её на две части, которые называются полуплоскостями. Полуплоскость – это часть плоскости, лежащая по одну сторону от любой прямой на этой плоскости. Луч — это частьпрямой, состоящая из всех точек этой прямой, лежащих по одну сторону от одной её точки. Эта точка называется началом луча.

Первый признак равенства треугольников.

Доказать, что треугольник ABC равен треугольнику DEF.

Доказательство:

1. Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.

2. При этом отрезки СА и СВ наложатся на отрезки FE и FD.

3. А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.

4. Это в свою очередь даст совмещение вершин А и D, В и Е.

5. Следовательно, треугольники полностью совместятся, а значит, они равны.

Теорема доказана.

3. Задача по теме " Сумма углов треугольника".

В треугольнике ABC даны два угла: 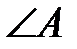=32º, =57º. Найдите третий угол.

Билет № 7

Угол (определение). Измерение углов. Основные свойства измерения углов.

У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла).

За единицу измерения углов обычно принимается угол, составляющий одну сто восьмидесятую часть развернутого угла. Считают, что величина этого угла равна одному градусу, обозначают 1^о.

Градусная величина угла показывает, сколько раз угол в один градус и его части укладываются в этом угле. Прибор для измерения транспортир.

1)Каждый угол имеет определенную градусную меру большую нуля.

2)Развернутый угол равен 180 градусам.

3) Градусная мера угла равна сумме градусных мер углов,на которые он разбивается любым лучом,проходящим между его сторонами.

Второй признак равенства треугольника.

(Второй признак равенства треугольников — по стороне и двум прилежащим к ней углам)

Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.

Дано:ΔABC, ΔA₁B₁C₁, AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁.

Доказать: ΔABC= ΔA₁B₁C₁

Доказательство:

Так как AB=A₁B₁, то треугольник A₁B₁C₁ можно наложить на треугольник ABC так, чтобы

· сторона A₁B₁ совместилась со стороной AB,

· точки C₁ и С лежали по одну сторону от прямой AB.

Поскольку ∠A=∠A₁, сторона A₁С₁ при этом наложится на луч AC.

Так как ∠B=∠B₁, сторона B₁C₁ наложится на сторону BC.

Точка С₁ принадлежит как стороне A₁С₁, так и стороне B₁C₁, поэтому С₁лежит и на луче AC, и на луче CB.

Лучи AC и CB пересекаются в точке C. Следовательно, точка С₁ совместится с точкой C.

Значит, сторона A₁С₁ совместится со стороной AC, а сторона B₁C₁ — со стороной BC.

Таким образом, при наложении треугольники ABC и A₁B₁C₁полностью совместятся.

А это означает, что ΔABC= ΔA₁B₁C₁ (по определению).

Что и требовалось доказать.

3. Задача по теме " Высота, медиана и биссектриса треугольника".

Отрезок СЕ является медианой ACD. Известно, что AE=2,5 см, AC=3 см, CD=4 см. Найдите периметр треугольника ACD.

Билет № 8

Дата добавления: 2018-05-12; просмотров: 4747; Мы поможем в написании вашей работы!

Поделиться с друзьями:

⇐ Предыдущая 123 4 5 6 7 8 9 Следующая ⇒

Мы поможем в написании ваших работ!