Перпендикулярные прямые (определение). Перпендикуляр к прямой.
Две прямые называются перпендикулярными, если они пересекаются под прямым углом
. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Построение биссектрисы угла.

Построить биссектрису данного угла.

| Из вершины A данного угла как из центра описываем окружность произвольного радиуса r. Пусть B и С – точки ее пересечения со сторонами угла. |

Из точек В и С проведем окружности тем же радиусом r. Пусть точка D – точка их пересечения отличная от A.
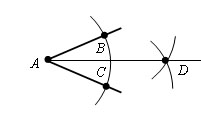
Проведем луч AD.

Проведем отрезки BD и CD. Δ ABD = Δ ACD, по третьему признаку равенства треугольников. Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC.
3. Задача по теме "Свойства равнобедренного треугольника".
В равнобедренном треугольнике ABC AE – высота, BC- основание. Известно, что BC=12,8 см. Найдите длину отрезка CE.
Билет № 14
Виды треугольников по величине углов.

| Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º). |

| Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º). |

| Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º). |
Деление отрезка пополам.
|
|
|

| Пусть AB данный отрезок. Описываем окружность радиусом AB с центром в точках A и B. Пусть эти окружности пересекаются в точках С1 и С2. |

| Точки С1 и С2 лежат в разных полуплоскостях от прямой AB. Проведем через точки С1 и С2 прямую. Пусть она пересекает прямую AB в некоторой точке О. Точка О – средина отрезка AB. |

| Док-во. Δ C1AC2 = Δ C1BC2 по третьему признаку равенства треугольников (AC1 = BC1, AC2 = BC2, по построению и С1С2 - общая). Поэтому ∠ AC1C2 = ∠ BC1C2. Отсюда следует Δ AC1O = Δ BC1O по второму признаку равенства треугольников (∠ AC1C2 = ∠ BC1C2, AC1 = BC1 по построению, OC1 – общая). Следовательно AO = OB и O – середина отрезка AB. |
3. Задача по теме " Смежные углы".
Найдите смежные углы, если один из них в два раза больше другого.
Билет № 15
Расстояние от точки до прямой. Расстояние между параллельными прямыми.
Расстояние от точки до прямой — это длина перпендикуляра, опущенного из данной точки на данную прямую.
Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Поэтому, чтобы найти расстояние между параллельными прямыми, надо:
1) выбрать на одной из параллельных прямых точку;
2) опустить из выбранной точки к другой прямой перпендикуляр;
|
|
|
3) найти длину этого перпендикуляра.
Неравенство треугольника.
Теорема.
Каждая сторона треугольника меньше суммы двух других сторон.
Доказательство.
Рассмотрим произвольный треугольник ABC и докажем, что AB<AC+СB. Отложим на продолжении стороны AC отрезок СD, равный стороне СB.

| В равнобедренном треугольнике BCD 1 = 2, а в треугольнике ABD угол ABD > 1 и, значит, угол ABD > 2. Так как в треугольнике против большего угла лежит большая сторона, то AB < AD. Но AD = AC + CD = AC + CB, поэтому AB < AC + CB. Теорема доказана. |
Следствие.
Для любых трех точек A, B и С, не лежащих на одной прямой, справедливы неравенства: AB < AC + CB, AC < AB + BC, BC < BA + AC.
3. Задача по теме " Взаимное расположение окружностей".
Две окружности диаметром 4 и 8 см касаются внешним образом. Найдите расстояние между центрами этих окружностей.
Билет № 16
Дата добавления: 2018-05-12; просмотров: 1883; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!
