Треугольник (определение). Равные треугольники. Существование треугольника, равному данному.
Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
Точки называются вершинами треугольника. Соединяющие вершины отрезки называются сторонами треугольника. Треугольник обозначается указанием его вершин.
Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
Каков бы ни был треугольник, существует треугольник, равный данному, отложенный в треугольника, равного данному. заданном направлении, относительно заданной полупрямой.
Третий признак равенства треугольника.
(Третий признак равенства треугольников — по трём сторонам)
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Дано:
ΔABC,
ΔA1B1C1,
AB=A1B1, AC=A1C1, BC=B1C1.
Доказать:
ΔABC= ΔA1B1C1
Доказательство:
Приложим треугольник A1B1C1 к треугольнику ABC так, чтобы
· вершина A1 совместилась с вершиной A,
· вершина B1 совместилась с вершиной B,
· точки C1 и C лежали по разные стороны от прямой AB.
При этом возможны три случая взаимного расположения луча CC1 и угла ACB.
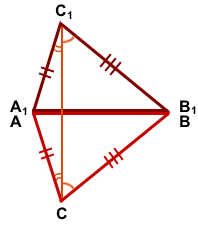I. Луч CC1 проходит внутри угла ACB.
Проведём отрезок CC1.
По условию AC=A1C1 и BC=B1C1, поэтомутреугольники ACC1 и BCC1 — равнобедренные с основанием CC1.
По свойству равнобедренного треугольника, ∠ACC1=∠AC1C и ∠BCC1=∠BC1C.
Если к равным углам прибывать равные углы, то получим равные углы:
|
|
|
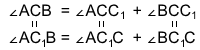
Таким образом, ∠ACB=∠AC1B.
Точки A1 и A, B1 и B совмещены, то есть ∠AC1B и ∠A1C1B1 — один и тот же угол.
Для треугольников ABC и A1B1C1 имеем:
AC=A1C1, BC=B1C1 (по условию), ∠ACB=∠A1C1B1 (по доказанному).
Следовательно, ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
II. Луч CC1 проходит внутри угла ACB.
Так как AC=A1C1 и BC=B1C1, треугольники ACC1и BCC1 — равнобедренные с основанием CC1 и ∠ACC1=∠AC1C и ∠BCC1=∠BC1C (как углы при основании).
Если из равных углов вычесть равные углы, то получим равные углы:
Таким образом, ∠ACB=∠AC1B и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
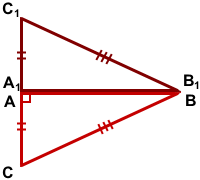III. Луч CC1 совпадает со стороной угла ACB.
По условию BC=B1C1, поэтому треугольник BCC1 — равнобедренный с основанием CC1.
Отсюда ∠C1=∠C (как углы при основании) и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Что и требовалось доказать.
3. Задача по теме "Неравенства треугольника".
Существует ли треугольник со сторонами 7 см, 2 см и 10 см? Ответ обоснуйте.
Билет № 9
Углы, образованные при пересечении двух прямых секущей. Аксиома параллельности прямых (без доказательства)
При пересечении прямых секущей образуются такие пары углов:
|
|
|
· Углы, лежащие между прямыми и по одну сторону секущей, называются внутренними односторонними углами.
· Углы, лежащие между прямыми и по разные стороны от секущей, называются внутренними разносторонними углами.
· Углы, лежащие по одну сторону секущей, но один из них лежит между заданными прямыми, а другой не лежит между ними, называются соответствующими.
Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной
Дата добавления: 2018-05-12; просмотров: 2980; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!