Глава 13. ІНТЕНСИВНІСТЬ ТА ШИРИНА СПЕКТРАЛЬНИХ ЛІНІЙ
Ймовірність переходів
Розглянемо систему з двома енергетичними рівнями  і
і  (рис.13.1), на кожному із яких знаходиться
(рис.13.1), на кожному із яких знаходиться  і
і  електронів. Їх енергетична ієрархія може бути якісно оцінена за правилами Хунда (Гунда), які розглядались раніше у 11-й главі.
електронів. Їх енергетична ієрархія може бути якісно оцінена за правилами Хунда (Гунда), які розглядались раніше у 11-й главі.
|
|
Значення  і
і  знаходять експериментально або із розрахунків, наприклад методом стаціонарної теорії збурень, яка застосовувалась у попередній главі при розгляді рівнів атомів гелію. Між рівнями
знаходять експериментально або із розрахунків, наприклад методом стаціонарної теорії збурень, яка застосовувалась у попередній главі при розгляді рівнів атомів гелію. Між рівнями  і
і  можуть відбуватися три різновиди електронних переходів: 1) - вимушений перехід
можуть відбуватися три різновиди електронних переходів: 1) - вимушений перехід  з поглинанням кванта
з поглинанням кванта  ; 2) - вимушений перехід
; 2) - вимушений перехід  з випромінюванням кванта
з випромінюванням кванта  ; 3) - спонтанний перехід
; 3) - спонтанний перехід  з випромінюванням кванта
з випромінюванням кванта  . Позначимо кількість таких переходів за одиницю часу через
. Позначимо кількість таких переходів за одиницю часу через  і
і  відповідно. Вони зв’язані з коефіцієнтами Ейнштейна
відповідно. Вони зв’язані з коефіцієнтами Ейнштейна  :
:
 (13.1)
(13.1)
 (13.2)
(13.2)
 , (13.3)
, (13.3)
де  - спектральна густина випромінювання, віднесена до одиничного інтервалу частот [ерг·с/cм3]. Коефіцієнти Ейнштейна характеризують даний електронний перехід. Вони визначають імовірності переходів, хоча і відрізняються від безрозмірних математичних ймовірностей, бо
- спектральна густина випромінювання, віднесена до одиничного інтервалу частот [ерг·с/cм3]. Коефіцієнти Ейнштейна характеризують даний електронний перехід. Вони визначають імовірності переходів, хоча і відрізняються від безрозмірних математичних ймовірностей, бо  і
і  - імовірності переходів за одиницю часу і тому мають розмірності [c-1] і [см-3×ерг-1×с-2] відповідно. Ці коефіцієнти зв’язані між собою, бо у стані рівноваги має місце співвідношення:
- імовірності переходів за одиницю часу і тому мають розмірності [c-1] і [см-3×ерг-1×с-2] відповідно. Ці коефіцієнти зв’язані між собою, бо у стані рівноваги має місце співвідношення:
 (13.4)
(13.4)
Для встановлення зв’язку між коефіцієнтами Ейнштейна підставимо у (13.4) вирази (13.1), (13.2) і (13.3), розв’яжемо рівняння відносно  і порівняємо з формулою Планка для спектральної густини випромінювання абсолютно чорного тіла:
і порівняємо з формулою Планка для спектральної густини випромінювання абсолютно чорного тіла:
 .
.
З урахуванням, що за розподілом Больцмана  , остаточно отримаємо:
, остаточно отримаємо:
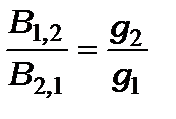 , (13.5)
, (13.5)
 , (13.6)
, (13.6)
де 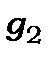 і
і  - статистичні ваги (ступені виродження) рівнів
- статистичні ваги (ступені виродження) рівнів  і
і  . Із співвідношення (13.6) видно, що інтенсивність спонтанних переходів пропорційна кубу частоти, тому при дуже низьких частотах основну роль відіграють вимушені переходи.
. Із співвідношення (13.6) видно, що інтенсивність спонтанних переходів пропорційна кубу частоти, тому при дуже низьких частотах основну роль відіграють вимушені переходи.
Золоте правило Фермі
Імовірність вимушених переходів wіf із початкового стану і до
кінцевого стану  за одиницю часу залежить від інтенсивності світла, що його викликає. При не дуже великих інтенсивностях світла доведення формули
за одиницю часу залежить від інтенсивності світла, що його викликає. При не дуже великих інтенсивностях світла доведення формули  розглядається в квантовій механіці за допомогою нестаціонарної теорії збурень і визначається золотим правилом Фермі
розглядається в квантовій механіці за допомогою нестаціонарної теорії збурень і визначається золотим правилом Фермі
 , (13.7)
, (13.7)
де ω - кругова частота коливань електромагнітної хвилі,  і
і  - енергії у стаціонарних станах
- енергії у стаціонарних станах  і
і  відповідно
відповідно 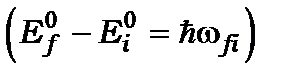 , а
, а  - матричний елемент оператора збурення
- матричний елемент оператора збурення 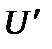
 , (13.8)
, (13.8)
а  - хвильові функції незбуреної системи в її кінцевому і початковому стаціонарних станах відповідно.
- хвильові функції незбуреної системи в її кінцевому і початковому стаціонарних станах відповідно.
============================================================
Знайдемо ймовірність вимушеного електронного переходу  методом нестаціонарної теорії збурень під дією електромагнітної хвилі
методом нестаціонарної теорії збурень під дією електромагнітної хвилі
 (13.д.1)
(13.д.1)
Розмір атома  тому наближено
тому наближено  Електричне поле хвилі створює потенціал
Електричне поле хвилі створює потенціал 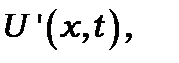 що збурює атом протягом інтервалу часу
що збурює атом протягом інтервалу часу  від
від  t0 до
t0 до  .
.
 . (13.д.2)
. (13.д.2)
Рівняння Шредінґера для випадку збурення, має вигляд
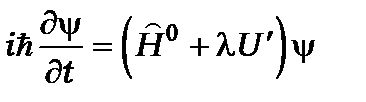 , (13.д.3)
, (13.д.3)
де 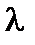 - довільне позитивне число, менше одиниці. Для випадку
- довільне позитивне число, менше одиниці. Для випадку 
 , (13.д.4)
, (13.д.4)
де
 . (13.д.5)
. (13.д.5)
 - характеризує ймовірність знаходження електрона в квантовому стані n.
- характеризує ймовірність знаходження електрона в квантовому стані n.
При наявності збурення  шукатимемо розв’язок (13.д.4) у вигляді
шукатимемо розв’язок (13.д.4) у вигляді
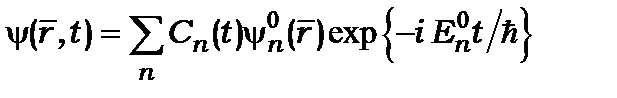 (13.д.6)
(13.д.6)
методом варіації змінного коефіцієнта Підстановкою (13.д.6) в (13.д.3) з урахуванням (13.д.4) отримаємо:
Підстановкою (13.д.6) в (13.д.3) з урахуванням (13.д.4) отримаємо:
 . (13.д.7)
. (13.д.7)
Помножимо обидві частини рівняння (13.д.7)  і проінтегруємо по всьому простору:
і проінтегруємо по всьому простору:
 (13.д.8)
(13.д.8)
 , (13.д.8*)
, (13.д.8*)
де використано:
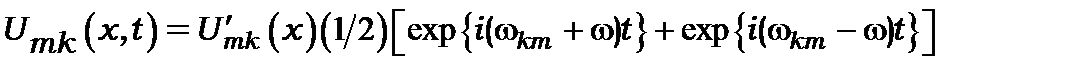 (13.д.9)
(13.д.9)
 (13.д.9*)
(13.д.9*)
 (13.д.10)
(13.д.10)
 (13.д.11)
(13.д.11)
У подальшому будемо називати 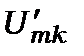 матричним елементом оператора збурення
матричним елементом оператора збурення 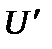 .
.
Система рівнянь (13.д.8*) точна, але її розв'язок отримати досить складно, тому наступним кроком є наближене представлення коефіцієнтів  – амплітуд імовірності за допомогою ряду
– амплітуд імовірності за допомогою ряду
 (13.д.12)
(13.д.12)
Параметр λ вказує на порядок малості. У відсутності збурення (в нульовому наближенні) усі поправки, починаючи з  , дорівнюють нулю
, дорівнюють нулю  для
для  , а
, а
 , (13.д.12*)
, (13.д.12*)
бо при  система дійсно знаходиться у початковому стані з імовірністю рівною одиниці.
система дійсно знаходиться у початковому стані з імовірністю рівною одиниці.
Рівняння (13.д.8*) із урахуванням (13.д.12*) зводяться до системи рівнянь
 (13.д.13)
(13.д.13)
У першому наближенні залишається лише перше рівняння
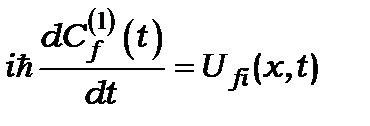 , (13.д.13*)
, (13.д.13*)
розв’язок якого дає амплітуду ймовірності переходу із початкового стану  в кінцевий
в кінцевий 
 . (13.д.13**)
. (13.д.13**)
Після інтегрування (13.д.13*) у межах від  до
до  , де
, де  - інтервал часу дії збурення, отримаємо суму двох членів, в одному з яких у знаменнику стоїть
- інтервал часу дії збурення, отримаємо суму двох членів, в одному з яких у знаменнику стоїть  , а в другому -
, а в другому -  . Врахувавши, що для поглинання світла
. Врахувавши, що для поглинання світла  , отримаємо
, отримаємо
 (13.д.14)
(13.д.14)
 (13.д.15)
(13.д.15)
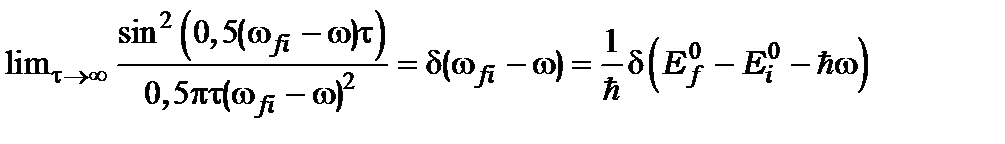 (13.д.16)
(13.д.16)
Підставивши (13.д.15) в (13.д.14), маємо
 . (13.д.17)
. (13.д.17)
Імовірність переходу із стану і до іншого стану f за одиницю часу дорівнює
 (13.д.18)
(13.д.18)
Цей вираз називається золотим правилом Фермі.
============================================================
Для того, щоб за допомогою золотого правила Фермі (13.7) знайти коефіцієнт вимушеного переходу Ейнштейна, необхідно знати потенціал збурення  та спектральну густину випромінювання
та спектральну густину випромінювання  , що збурює систему. Для плоскої електромагнітної хвилі з довжиною хвилі
, що збурює систему. Для плоскої електромагнітної хвилі з довжиною хвилі  (у довгохвильовому наближенні), де
(у довгохвильовому наближенні), де  – розмір атома, матричний елемент оператора збурення
– розмір атома, матричний елемент оператора збурення  згідно (13.д.2) дорівнює:
згідно (13.д.2) дорівнює:
 , (13.9)
, (13.9)
де  - напруженість електричного поля електромагнітної хвилі, що збурює, а
- напруженість електричного поля електромагнітної хвилі, що збурює, а 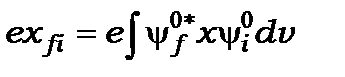 - матричний елемент дипольного моменту. Спектральна густина випромінювання запишеться за допомогою відомих формул електродинаміки
- матричний елемент дипольного моменту. Спектральна густина випромінювання запишеться за допомогою відомих формул електродинаміки
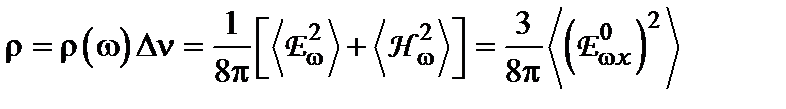 , (13.10)
, (13.10)
де квадрати  - середні значення квадратів напруженості електричного і магнітного полів,
- середні значення квадратів напруженості електричного і магнітного полів,  і для ізотропного випромінювання
і для ізотропного випромінювання  .
.
Комбінуючи (13.9) та (13.10), отримаємо
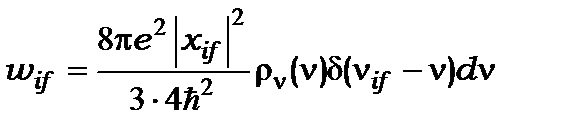 , (13.11)
, (13.11)
де використано, що  і
і  .
.
Після інтегрування по всім частотам маємо
 . (13.12)
. (13.12)
Згідно (13.2),
 (13.13)
(13.13)
Порівнюючи вирази (13.12) і (13.13), остаточно отримаємо вираз для коефіцієнта вимушених переходів Ейнштейна
 (13.14)
(13.14)
Таким чином, знаючи хвильові функції початкових  та кінцевих
та кінцевих 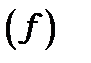 (f) стаціонарних станів, можна знайти матричні елементи переходу
(f) стаціонарних станів, можна знайти матричні елементи переходу  і коефіцієнти Ейнштейна
і коефіцієнти Ейнштейна  та
та  , які описують відповідно поглинання та випромінювання світла.
, які описують відповідно поглинання та випромінювання світла.
Для неполяризованого випромінювання (або при круговій поляризації) густина випромінювання збільшується вдвічі, тому що при круговій поляризації є дві взаємо перпендикулярні складові  і
і  і тому
і тому  .
.
Сила осцилятора
Для характеристики здатності систем випромінювати або поглинати електромагнітні хвилі використовують силу осцилятора  . Силою осцилятора називається безрозмірна величина - відношення інтенсивності випромінювання системою до інтенсивності випромінювання електрона, який розглядається, як затухаючий осцилятор, тобто
. Силою осцилятора називається безрозмірна величина - відношення інтенсивності випромінювання системою до інтенсивності випромінювання електрона, який розглядається, як затухаючий осцилятор, тобто
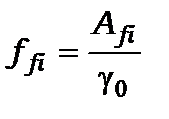 , (13.15)
, (13.15)
де  і -
і - 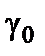 - коефіцієнти спонтанного випромінювання Ейнштейна та коефіцієнта затухання електрона, як осцилятора, відповідно. Згідно класичній електродинаміці середня енергія випромінювання гармонічного осцилятора, що коливається з частотою
- коефіцієнти спонтанного випромінювання Ейнштейна та коефіцієнта затухання електрона, як осцилятора, відповідно. Згідно класичній електродинаміці середня енергія випромінювання гармонічного осцилятора, що коливається з частотою 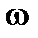 , визначається за формулою
, визначається за формулою
 , (13.16)
, (13.16)
де  - швидкість світла,
- швидкість світла,  - модуль другої похідної по часу від дипольного моменту, а
- модуль другої похідної по часу від дипольного моменту, а  і
і  - частота і амплітуда коливань осцилятора відповідно. За час
- частота і амплітуда коливань осцилятора відповідно. За час  енергія осцилятора зменшується на величину
енергія осцилятора зменшується на величину  . Тому енергія w, що випромінюється осцилятором, зв’язана з середньою енергією співвідношенням:
. Тому енергія w, що випромінюється осцилятором, зв’язана з середньою енергією співвідношенням:
 (13.17)
(13.17)
Після підстановки в (13.17)  із (13.16) і квадрату амплітуди
із (13.16) і квадрату амплітуди  із виразу для повної енергії осцилятора
із виразу для повної енергії осцилятора  остаточно отримаємо:
остаточно отримаємо:
 . (13.18)
. (13.18)
Тут g0 - коефіцієнт затухання коливань осцилятора, обернено пропорційний середньому часу життя  або кількості переходів за одиницю часу
або кількості переходів за одиницю часу
 (13.19)
(13.19)
Кількість переходів за одиницю часу визначає коефіцієнт випромінювання Ейнштейна, який, згідно (13.19), для гармонічного осцилятора
 . (13.20)
. (13.20)
Комбінуючи (13.6), (13.14), (13.15), отримаємо вираз для сили осцилятора атомної системи:
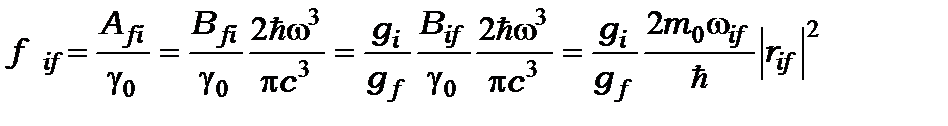 . (13.21)
. (13.21)
Сили осциляторів залежать від природи переходів. Вони наближаються до 1 для дозволених переходів, і малі (~10-5) для заборонених переходів. Знаючи  системи, можна знайти дисперсійну залежність для показника заломлення
системи, можна знайти дисперсійну залежність для показника заломлення
 . (13.22)
. (13.22)
де  - концентрація осциляторів у системі. Тому сили осциляторів дуже часто використовуються для характеристики оптичних властивостей різноманітних систем.
- концентрація осциляторів у системі. Тому сили осциляторів дуже часто використовуються для характеристики оптичних властивостей різноманітних систем.
Поглинання світла
Розглянемо розповсюдження світла в однорідному середовищі вздовж осі  . Обмежимося розглядом одновимірного випадку рис.13.2.
. Обмежимося розглядом одновимірного випадку рис.13.2.
|
Рис.13.2. До виведення закону Бугера |
Виберемо вздовж осі 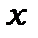 такий тонкий шар товщиною
такий тонкий шар товщиною  , що в ньому можна знехтувати зміною кількості атомів у стані 1 (тобто
, що в ньому можна знехтувати зміною кількості атомів у стані 1 (тобто  в інтервалі від
в інтервалі від  до
до  не змінюється). Коли можна знехтувати спонтанним випромінюванням
не змінюється). Коли можна знехтувати спонтанним випромінюванням 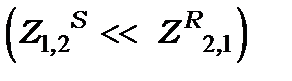 , то зменшення кількості квантів при взаємодії випромінювання з шаром речовини товщиною
, то зменшення кількості квантів при взаємодії випромінювання з шаром речовини товщиною  визначається за допомогою співвідношення :
визначається за допомогою співвідношення :

Підставимо в цей вираз значення 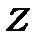 із (13.1 - 13.3) і помножимо його ліву і праву частини на
із (13.1 - 13.3) і помножимо його ліву і праву частини на 
 , (13.23)
, (13.23)
де  - зміна інтенсивності світлового потоку після проходження шару речовини товщиною
- зміна інтенсивності світлового потоку після проходження шару речовини товщиною  , а
, а  - світловий потік у точці з координатою
- світловий потік у точці з координатою  . Інтегруванням (13.23) отримаємо закон Бугера
. Інтегруванням (13.23) отримаємо закон Бугера
 , (13.24)
, (13.24)
де  світловий потік у точці з координатою
світловий потік у точці з координатою  , а
, а  – лінійний коефіцієнт ослаблення інтенсивності світла після проходження ним шляху довжиною x у речовині
– лінійний коефіцієнт ослаблення інтенсивності світла після проходження ним шляху довжиною x у речовині
 . (13.25)
. (13.25)
Експериментально визначають площу під спектральною лінією поглинання, із якої за допомогою (13.25) можна знайти коефіцієнт Ейнштейна, якщо 
 (13.25*)
(13.25*)
або силу осцилятора системи, використовуючи для цього (13.21).
Аналіз (13.25) показує, що є два випадки: малих і великих збуджень. При малих збудженнях, коли  , то
, то 
 і відбувається ослаблення інтенсивності світла при проходженні його у речовині.
і відбувається ослаблення інтенсивності світла при проходженні його у речовині.
При великих рівнях збудження - великих  , коли
, коли  порушується термодинамічна рівновага й виникає стан інверсної населеності. Цей випадок умовно в літературі називається випадком від’ємних температур, бо стан
порушується термодинамічна рівновага й виникає стан інверсної населеності. Цей випадок умовно в літературі називається випадком від’ємних температур, бо стан  має місце тільки формально при
має місце тільки формально при  . При «
. При «  », коефіцієнт поглинання світла стає негативним
», коефіцієнт поглинання світла стає негативним  і замість вбирання відбувається підсилення світла
і замість вбирання відбувається підсилення світла
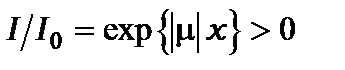 . (13.26)
. (13.26)
Явище підсилення світла в речовині, що знаходиться в стані інверсної населеності, знайшло широке застосування при побудові лазерів (розділ 13.7).
Дата добавления: 2018-05-09; просмотров: 409; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 Рис.13.1. Система із 2-х рівнів.
Рис.13.1. Система із 2-х рівнів.