Рівняння Шредінґера для двохелектронного атома
Потенціальна енергія електронів для двохелектронного атома, наприклад, атома гелію має вигляд:
 . (12.1)
. (12.1)

Рис.12.1. Схема моделі атома гелію.
Тут  - відстані від першого та другого електронів до центра ядра (рис.12.1) й відстань між електронами відповідно,
- відстані від першого та другого електронів до центра ядра (рис.12.1) й відстань між електронами відповідно,  - сума потенціальних енергій 1-го і 2-го електронів у полі ядра, а
- сума потенціальних енергій 1-го і 2-го електронів у полі ядра, а 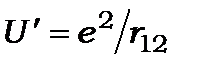 - потенціальна енергія взаємодії електронів.
- потенціальна енергія взаємодії електронів.
Рівняння Шредінґера для стаціонарних станів атома Не запишемо з урахуванням потенціалу взаємодії електронів між собою (12.1) за допомогою гамільтоніана системи  , де
, де  - гамільтоніани 1-го і 2-го електронів відповідно, а Dr1 і Dr2 - лапласіани, що залежать від координат 1-го і 2-го електронів.
- гамільтоніани 1-го і 2-го електронів відповідно, а Dr1 і Dr2 - лапласіани, що залежать від координат 1-го і 2-го електронів.
 , (12.2)1
, (12.2)1
Рівняння (12.2) можна розкласти на два незалежних рівняння, якщо знехтувати членом, що характеризує взаємодію електронів між собою  і шукати розв’язок у вигляді добутку хвильових функцій
і шукати розв’язок у вигляді добутку хвильових функцій  :
:
 , (12.3)
, (12.3)
Ці рівняння аналогічні відповідним рівнянням Шредінґера для атома водню, розв’язок яких ми вже розглядали раніше у 8 главі. Для них ми знайшли власні значення  та
та  і власні функцій
і власні функцій  та
та  . Розв’язок рівняння (12.2)
. Розв’язок рівняння (12.2)
 , (12.4)
, (12.4)
де нульовими індексами позначені хвильові функції і власні енергії для атома водню.
Метод збурень
Повний розв’язок рівняння (12.2) досить складний, тому використаємо метод збурення, коли 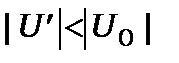 . Будемо шукати розв’язок рівняння (12.2) у вигляді
. Будемо шукати розв’язок рівняння (12.2) у вигляді
|
|
|
 , 12.5)
, 12.5)
де e - будь-яке мале число2  , а
, а  . Підставимо (12.5) в (12.2)
. Підставимо (12.5) в (12.2)
 (12.6)
(12.6)
Згадавши, що  та
та 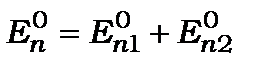 є розв’язком рівняння Шредінґера для не збуреного випадку, а також знехтувавши членами другого порядку малості
є розв’язком рівняння Шредінґера для не збуреного випадку, а також знехтувавши членами другого порядку малості  можна спростити рівняння (12.6)
можна спростити рівняння (12.6)
 . (12.7)
. (12.7)
Помножимо обидві частини (12.7) на  і проінтегруємо по всьому об’єму
і проінтегруємо по всьому об’єму
 . (12.8)
. (12.8)
Для розв’язку рівняння (12.8) використаємо самоспряженість оператора Гамільтона:
 . (12.9)4
. (12.9)4
Після підстановки (12.9) у (12.8) і згадавши, що  , остаточно отримаємо
, остаточно отримаємо
 12.10)
12.10)
та  (12.11)
(12.11)
Таким чином, поправку до енергії стаціонарного стану знаходять як середнє від потенціалу збурення  .
.
Для того щоб знайти хвильові функції, необхідно шукати розв’язок при наявності збурення у вигляді степеневого ряду
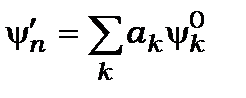 (12.12)
(12.12)
Для цього підставляємо (12.12) в формулу (12.7) і скориставшись співвідношенням
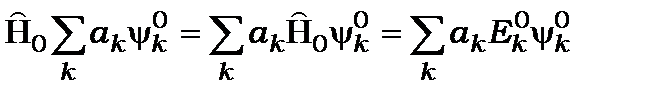 (12.13)
(12.13)
остаточно отримаємо
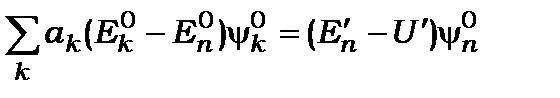 . (12.13*)
. (12.13*)
|
|
|
В формулі (12.13*) функції  є розв’язком рівняння Шредінгера, коли не враховується взаємодія електронів тобто, коли
є розв’язком рівняння Шредінгера, коли не враховується взаємодія електронів тобто, коли  . Із (12.13*) легко визначити коефіцієнти ряду
. Із (12.13*) легко визначити коефіцієнти ряду 
 . (12.14)
. (12.14)
Метод теорії збурень виправданий лише тоді, коли кожний послідовний член ряду (12.12) виявиться меншим попереднього, тобто коли виконується умова  і ряд (12.12) збігається. Крім того, ця теорія збурень незастосовна у випадку вироджених рівнів, коли
і ряд (12.12) збігається. Крім того, ця теорія збурень незастосовна у випадку вироджених рівнів, коли 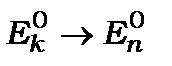 .
.
Розглянемо теперстаціонарні стани атома гелію. Для визначення енергії стаціонарного стану  атома гелію застосуємо формулу (12.10). Скористаємося для цього хвильовою функцією
атома гелію застосуємо формулу (12.10). Скористаємося для цього хвильовою функцією  стану атома водню, для якого
стану атома водню, для якого
 (12.15)
(12.15)
Формулою для потенціальної енергії взаємодії електронів між собою
 (12.16)
(12.16)
і підставимо їх в формулу (12.10) для 
 (12.17)
(12.17)
Шестикратний інтеграл (12.17) дорівнює 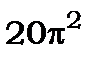 (розв`язок інтеграла дивись в додатку №2 [4].
(розв`язок інтеграла дивись в додатку №2 [4].
============================================================
Для обчислення квадратури в (12.17) перейдемо до нових змінних 

Почнемо інтегрування в формулі (12.17) по j1 і q1
 , де
, де  . Інтеграл I1 береться, якщо зробити заміну змінних:
. Інтеграл I1 береться, якщо зробити заміну змінних:  і
і  .
.
|
|
|
тоді 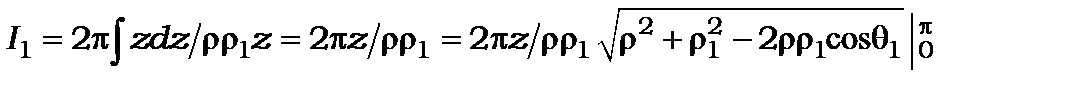 . Корінь треба брати так, щоб підкорінний вираз був більший нуля, тому
. Корінь треба брати так, щоб підкорінний вираз був більший нуля, тому  для
для  і
і 
 Здійснимо тепер інтегрування по dr1.
Здійснимо тепер інтегрування по dr1.
 Повний шестикратний інтеграл рівний
Повний шестикратний інтеграл рівний 
=============================================================
Після обчислення інтегралу остаточно отримаємо
 , (12.18)
, (12.18)
де 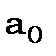 - радіус першої борівської орбіти.
- радіус першої борівської орбіти.
 .
.
Експеримент дає для цієї енергії значення  . Похибка між розрахунком і експериментом становить ~ 5,3%. Наступні порядки наближення зменшують розбіжність з експериментом.
. Похибка між розрахунком і експериментом становить ~ 5,3%. Наступні порядки наближення зменшують розбіжність з експериментом.
Принцип Паулі
Елементарні частинки мають однакові властивості, коли в них однакова маса, заряд, спін, енергія тощо. Тобто, якщо поміняти місцями дві однакові частинки, то нічого не зміниться. Ця властивість покладена в основу принципу нерозрізняємості або тотожності елементарних частинок.
Проте можна показати, що в системі двох електронів має місце обмінне виродження. Дійсно рівняння Шредінгера для двох тотожних не взаємодіючих частинок має такий вигляд:
 ,
,
а його розв’язки:
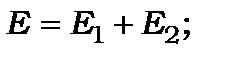
 ;
;  (12.19)
(12.19)
Із формул (12.19) бачимо, що існує два різних стани  і
і  з однаковою енергією
з однаковою енергією  , тобто має місце обмінне виродження, котре суперечить принципу тотожності однакових частинок.
, тобто має місце обмінне виродження, котре суперечить принципу тотожності однакових частинок.
|
|
|
Отже, треба знайти такі розв’язки рівняння Шредінгера, котрі не суперечать принципу тотожності однакових частинок. Для цього введемо оператор перестановки частинок  такий, що
такий, що
 20)
20)
Подіємо тепер на хвильову функцію оператором  двічі. Тоді
двічі. Тоді
 (12.21)
(12.21)
отримаємо початкову хвильову функцію. Тому
 (12.22)
(12.22)
Для двох можливих значень оператора  існують два різновиди хвильових функцій, а саме:
існують два різновиди хвильових функцій, а саме:
- симетричні, коли  , тобто
, тобто  і хвильова функція не змінює знака при перестановці двох тотожних частинок,
і хвильова функція не змінює знака при перестановці двох тотожних частинок,
- антисиметричні, коли  і хвильова функція змінює знак при перестановці місцями двох тотожних частинок.
і хвильова функція змінює знак при перестановці місцями двох тотожних частинок.
Сконструюємо такі хвильові функції, користуючись принципом суперпозиції:
 (12.23)
(12.23)
де кожна із складових хвильових функцій  і
і  обмінно вироджена. Лінійна комбінація симетричних та антисиметричних хвильових функцій
обмінно вироджена. Лінійна комбінація симетричних та антисиметричних хвильових функцій
 (12.24)
(12.24)
є також розв’язком вихідного хвильового рівняння Шредінґера, де  - сталі коефіцієнти. Знайдемо тепер густину ймовірності
- сталі коефіцієнти. Знайдемо тепер густину ймовірності 
 (12.25)
(12.25)
Застосуємо тепер до (12.25) принцип тотожності частинок. Згідно цього принципу перестановка частинок місцями не повинна змінити 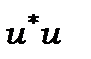 . Згадаємо також, що оператор
. Згадаємо також, що оператор  . Тому члени
. Тому члени  і
і  не змінюють знак, а члени, в які входить
не змінюють знак, а члени, в які входить  або
або  , змінюють знак при перестановці місцями частинок 1 і 2, тобто змінюється знак другого і третього членів в формулі (12.25). Для того щоб густина ймовірності
, змінюють знак при перестановці місцями частинок 1 і 2, тобто змінюється знак другого і третього членів в формулі (12.25). Для того щоб густина ймовірності  не змінювала знак при перестановці місцями двох частинок, необхідно вимагати, щоб мали місце такі співвідношення:
не змінювала знак при перестановці місцями двох частинок, необхідно вимагати, щоб мали місце такі співвідношення:  або
або  . Із цих співвідношень виникає альтернатива:
. Із цих співвідношень виникає альтернатива:
-чи  ,
,
чи  . (12.26)
. (12.26)
Умови (12.26) означають, що при 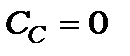 стан описується антисиметричними хвильовими функціями, а при
стан описується антисиметричними хвильовими функціями, а при  - симетричними. Який з цих станів реалізується в природі повинен дати відповідь дослід.
- симетричними. Який з цих станів реалізується в природі повинен дати відповідь дослід.
В 1924 році лауреат нобелівської премії швейцарський фізик Вольфганг Паулі узагальнив існуючий дослід і встановив, що для стани частинок з напівцілим спіном ( s = 1/2, 3/2, ...) описуються антисиметричними хвильовими функціями YA, а частинок з цілим спіном (s = 0, 1, 2,...) - симетричними хвильовими функціями  . Це твердження називається принципом Паулі або принципом виключення. Його можна сформулювати і інакше, а саме: в системі частинок з напівцілим спіном - ферміонів не може бути двох частинок, що знаходяться в одному і тому ж стані. Дійсно ферміони описуються антисиметричними функціями:
. Це твердження називається принципом Паулі або принципом виключення. Його можна сформулювати і інакше, а саме: в системі частинок з напівцілим спіном - ферміонів не може бути двох частинок, що знаходяться в одному і тому ж стані. Дійсно ферміони описуються антисиметричними функціями:
 (12.27)
(12.27)
де індекси при хвильових функціях означають трійку квантових чисел  ,
,  ,
,  для частинок з однаковим спіном. Якщо
для частинок з однаковим спіном. Якщо  , то і
, то і  тобто
тобто  і такого стану не існує. Аналогічно, коли
і такого стану не існує. Аналогічно, коли  , то
, то  і такого стану також не існує. Цей розгляд можна узагальнити для системи будь-якої скінченої
і такого стану також не існує. Цей розгляд можна узагальнити для системи будь-якої скінченої  кількості частинок. У цьому разі
кількості частинок. У цьому разі
 . (12.28)
. (12.28)
Якщо дві частинки тотожні, то це означає, що  . Отже, детермінант з однаковими рядками дорівнює нулеві, тобто
. Отже, детермінант з однаковими рядками дорівнює нулеві, тобто  й такого стану не існує.
й такого стану не існує.
В атомі стан електронів визначається 4-ма квантовими числами  ,
,  ,
,  l і
l і  або
або 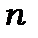 ,
,  ,
, 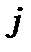 і
і  . В кожному із таких станів згідно принципу Паулі може знаходитись лише один електрон.
. В кожному із таких станів згідно принципу Паулі може знаходитись лише один електрон.
Стани бозонів - частинок з цілим спіном описуються симетричними функціями. Тому для них не існує додаткових умов. Отже, в одному стані може знаходитись довільна кількість бозонів.
Різні властивості ферміонів і бозонів виявляються і в поведінці їх ансамблів, а саме:
- ферміони описуються за допомогою статистики Фермі-Дірака, в якій функція розподілу має такий вигляд
| Рис.12.2. Функції енергетичного розподілу, |
 (12.29)
(12.29)
- бозони описуються за допомогою статистики Бозе-Ейнштейна, в якій функція розподілу має такий вигляд
 (12.30)
(12.30)
де Е - енергія частинок, Еі - хімічний потенціал стану частинок, котрий визначає зміну термодинамічних потенціалів при зміні числа частинок. Для того щоб відновити у пам’яті вигляд цих функцій розподілу, вони разом з розподілом Больцмана наведені на рис. 12.2, із якого видно, що вони дуже сильно відрізняються між собою особливо при малих значеннях  .
.
Зробимо ще одне зауваження. Принцип Паулі потрібно застосовувати до всіх частинок, що знаходяться у Всесвіті. Ця обставина може призводити до надзвичайно великих складнощів у визначені хвильових функцій, тому що потрібно було б враховувати існування безлічі частинок. Проте на практиці необхідно враховувати лише ті частинки, хвильові функції котрих перекриваються. Це значно спрощує задачу знаходження хвильових функцій, тому що  - функції досить швидко затухають із зростанням відстані між частинками r. В більшості практичних задач досить обмежитись врахуванням взаємодії частинок, що знаходяться на віддалях, що не більші за радіус першої борівської орбіти
- функції досить швидко затухають із зростанням відстані між частинками r. В більшості практичних задач досить обмежитись врахуванням взаємодії частинок, що знаходяться на віддалях, що не більші за радіус першої борівської орбіти  .
.
Дата добавления: 2018-05-09; просмотров: 482; Мы поможем в написании вашей работы! |

Мы поможем в написании ваших работ!

 .
.