Теорема об изменении кинетической энергии механической системы
Пусть есть механическая система, состоящая из n точек, для каждой точки запишем уравнение (10а) с учётом того, что на точки могу действовать как внешние, так и внутренние силы.
(10 б) – это теорема об изменении кинетической энергии для механической системы.
Формулировка:
Изменение кинетической энергии механической системы, на некотором перемещении её точек равно сумме работ внешних и внутренних сил, приложенных к точкам механической системы, на том же перемещении этих точек.
Билет №25.
Работа силы тяжести, силы упругости и вращающего момента.
Работа силы тяжести
Работа силы тяжести равна взятому со знаком «+» или «–» произведению силы тяжести 
(т.е. mg) на перемещение 
точки приложения силы 
, то есть
. (2)
В формуле (2) знак «+» соответствует опусканию, а знак «–» – подъему точки приложения силы .
| Следует подчеркнуть, что работа силы тяжести не зависит от вида траектории, по которой перемещается точка приложения этой силы. |
Работа силы упругости равна половине произведения жесткости упругого тела на разность квадратов его начального и конечного удлинений.
Если конечное удлинение пружины равняется нулю (x2 = 0), т. е. пружина приходит в недеформированное состояние, то она совершает работу
где x — начальное удлинение пружины.
Интересно, что работа силы упругости имеет некоторое сходство с работой силы тяжести. Если сравнить выражения для работы этих двух сил:
|
|
|
- работа силы тяжести
- работа силы упругости
то можно заметить, что в обоих случаях работа зависит от начального и конечного положении тела. В первой формуле высота h определяет положение тела, на которое действует сила тяжести (например, относительно поверхности Земли). Во второй формуле удлинение х определяет положение одного конца пружины относительно другого ее конца.
Работа как силы упругости, так и силы тяжести зависит не от формы, или длины пути, а только от начального и конечного положений движущегося тела.
РАБОТА ВРАЩАЮЩЕГО МОМЕНТА.
Определим мощность при вращательном движении
Мощность при вращательном движении тела равна произведению вращающего момента (момента пары) на угловую скорость.
Билет №26.
Принцип Даламбера. Уравнение кинетостатики.
Принцип Даламбера (для механической системы):
Любую систему сил можно рассматривать, как находящуюся в равновесии, если к этой системе добавить инерциальные нагрузки.
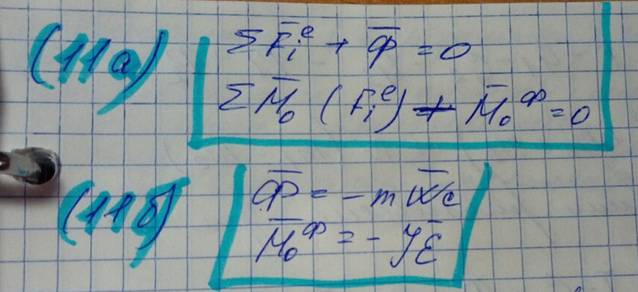
Из книжки(!):
Принцип Даламбера (для материальной точки):
Если в любой момент времени к действующим на точку активным силам и реакции связи присоединить силу инерции, то полученная система сил будет уравновешенной.
|
|
|
Где Fa – активные силы, N – реакция связи, Fи – силы инерции.
Принцип Даламбера (для механической системы):
Если в любой момент времени к каждой из точек системы кроме действующих на неё внешних и внутренних сил присоединить соответствующие силы инерции, то полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.
Уравнение кинетостатики (????):
Уравнения кинетостатики звена механизма, как твердого тела, в векторной форме имеют вид:
, 
,
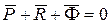Здесь 
, 
- главные векторы активных сил и сил реакций, приложенных к звену, 
- главный вектор сил инерции звена; 
- главные моменты активных сил и сил реакций относительно некоторого центра O, 
- главный вектор сил инерции звена относительно того же центра O. Главный вектор и главный момент сил инерции звена вычисляются по формулам:
, 
,
где 
- радиус-вектор, 
- ускорение центра масс, 
- ускорение центра O, m – масса звена; 
- угловая скорость, 
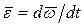- угловое ускорение звена, JO – тензор инерции звена относительно центра O. Таким образом, в каждый момент времени, действующие на звено силы уравновешиваются силами инерции звена, а моменты сил, приложенные к звену, уравновешиваются моментами сил инерции звена. Это утверждение представляет собой известный из теоретической механики принцип Даламбера, сформулированный по отношению к твердому телу.
|
|
|
В случае плоского механизма, вектор главного момента сил инерции звена относительно центра масс S будет определяться своими декартовыми координатами:
, 
, 
.
В проекциях на оси декартовой системы координат векторные уравнения кинетостатики звена равносильны шести скалярным уравнениям:
Если механизм плоский и Oxy – плоскость движения звеньев, то три из приведенной системы уравнений становятся тождественно равными нулю и остаются лишь три скалярных уравнения кинетостатики для каждого звена:
Таким образом, для пространственного механизма требуется составить и решить 
, а для плоского - 
скалярных уравнений кинетостатики, где n – число звеньев механизма. Эти системы уравнений могут быть решены аналитически, а в случае плоского механизма векторные уравнения сил удобно решать с помощью метода векторных планов. Для каждого нового положения механизма систему уравнений кинетостатики необходимо составлять и решать заново. Поэтому силовой расчет механизма является довольно трудоемкой задачей, решение которой целесообразно автоматизировать с помощью компьютера.
|
|
|
Билет №27.
Дата добавления: 2018-05-02; просмотров: 650; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!