К.П.Д РЕГУЛИРУЕМОГО ЭЛЕКТРОПРИВОДА
Все способы регулирования скорости электроприводов можно разделить на две группы. Первая группа включает способы регулирования, при которых скорость идеального холостого хода w0 электродвигателя остается постоянной.В эту группу входят электроприволы с ДПТ НВ, имеющими постоянное напряжение на якоре и номинальный магнитный поток при регулируемом сопротивлении якорной цепи,а также асинхронные электроприводы c номинальной частотой питающего напряжения и изменяемой величиной скольжения.
Вторая группа охватывает способы, где скорость идеального холостого хода w0 элекродвигателя изменяется с помощью управляющего воздействия (ДПТ с регулируемым напряжением на якоре или обмотке возбуждения, многоскоростные АД, частотное регулирование АД, каскадные схемы). Характер зависимости КПД регулируемого электропривода от нагрузки и диапазона регулирования скорости для указанных групп будет разный. Для выявления особенностей КПД регулируемого электропривода при w0 = const рассмотрим реостатное регулирование скорости ДПТ НВ.Запишем КПД ДПТ НВ в виде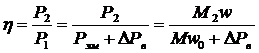 
,
Для двигательного режима момент на валу М2 можно выразить через электромагнитный момент М и потерю момента 
Для двигателей постоянного тока при регулировании скорости принимают
, тогда
,
где
|
|
|
При номинальном магнитном потоке 
и выражение для КПД принимает вид 
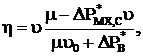(6.77)
где 
Как видно КПД является функцией относительной скорости ѵ и относительного момента µ Если определить диапазон регулирования скорости
при номинальном моменте, т. е. при µ = 1, то КПД
T. e. КПД электродвигателя изменяется практически обратно пропорционально диапазону регулирования скорости. При данной величине скорости (v= const) и изменении нагрузки (µ = var)КПД увеличивается при увеличении µ, приближаясь к величине v.
A теперь посмотрим, как будет изменяться КПД асинхронного двигателя при w0 = const и изменении угловой скорости ротора w0 за счет скольжения s.
Теперь рассмотрим КПД регулируемого электропривода при w0= var.
КПД регулируемого электродвигателя определяется отношением мощности на валу к потребляемой мощности:
Разделив числитель и знаменатель на Рном, найдем, что КПД
оптимальный коэффициент загрузки регулируемого электродвигателя
при этом следует иметь в виду, что относительная скорость υ ротора практически равна относительной частоте α питающего двигатель напряжения. Если ввести обозначения:
|
|
|
| 
|
НАГРЕВ И ОХЛАЖДЕНИЕ ЭЛЕКТРОДВИГАТЕЛЕЙ.
Потери электроэнергии в дв. превращаются в теплоту, вследствие чего дв. нагр. Части дв. при работе нагр. неодинаково. Выделение тепла в различныхреж. также неодинаково.
Для упрощения анализа тепловых процессов, происходящих вЭД, на основе допущений составляют тепловые модели. Наиболее простая модель основана на допущениях:
1) 
дв. представляет собой однородное в тепловом отношении тело, равномерно нагревающееся по всему объему за счет источника мощности 
,
2) теплоотдача во внешнюю среду пропорц. первой степени разности темп.тела и охл. среды,
3) темп.охл. среды постоянная.
Для такой модели (Рис.7.1) мощность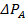 
теплового потока, передаваемая в окружающую среду, равна
, (7.3)где 
, (7.4)
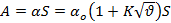, (7.5),где 
- температура перегрева,
А – теплоотдача в окружающую среду, Вт/оС;S – площадь поверхности охлаждения, м2;
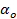- удельная теплоотдача при скорости охлаждающего воздуха 
, Вт/оС м2;
- скорость охлаждающего воздуха, м/с;К – эмпирический коэффициент, принимаемый для электрических машин, равным примерно 0,8.Величина, обратная теплоотдаче, называется тепловым сопр. 
,
Поэтому мощ. теплового потока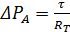 
,
|
|
|
Мощ. 
теплового потока, идущего на нагрев тела, определяется выражением
, (7.8) где 
, (7.9)
Суд – удельная теплоемкость, Дж/оС кг; m – масса тела, кг.По закону сохранения энергии 
,Или 
, (7.11)
Полученное дифференциальное уравн (7.11) теплового баланса в одномассовой модели аналогично уравнению 
, (7.12)
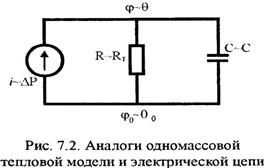В эл. цепи, показанной на 7.2, где имеем аналогии: ток 
~ тепл. поток 
, эл.сопр.R ~ тепл.сопр.RT, эл. емкость С ~ теплоемкость с, эле.потенциал 
~ тем. тела 
, эл. напр.u ~ темп. перегрева 
.
Поскольку для эл. цепи 7.2 пост.времени 
,
и установившееся значение напр. 
,
то (7.12) можно представить в виде 
,
Аналогично имеем для уравнения (7.11) тепловой модели 
, (7.16) 
, (7.17) 
(7.18)
где ТН – пост.времени нагрева, 
– установ. значение перегрева.Дифф.Уравн. (7.18) имеет решение 
, (7.19) где 
- нач.знач.Темп.перегр..
Нагрев или охл. тела определяется нач. знач.темп.: если 
, будет нагрев, если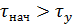 
- охл. (Рис.7.3).
Одномассовая тепловая модель ЭД простая и удобная для анализа, но она лишь прибл. отражает нагрев обмоток. С целью повышения точности расчетов применяют 2-хмассовую модель, разделяя нагрев статора и ротора ЭД. В этом случае, принимая потери мощ. в роторе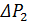 
и темп.внутр. поверхности статора 
постоянными, можем записать уравн.тепл. равновесия ротора 
, (7.28)где 
(7.29) 
, (7.30),где 
- темп. внутри ротора, m2 – масса ротора, С2.уд– удельная теплоемкость ротора,
|
|
|
RT2 – тепловое сопр. между проводниками ротора и внутренней поверхностью статора.
Решение (7.28) имеет вид 
, (7.31)
где 
(7.32) 
, (7.33)
- установившееся значение темп.перегрева ротора,
ТН2–постоянная времени нагрева ротора, 
- начальное значение темп.перегрева обмотки ротора
(7.33) Если 
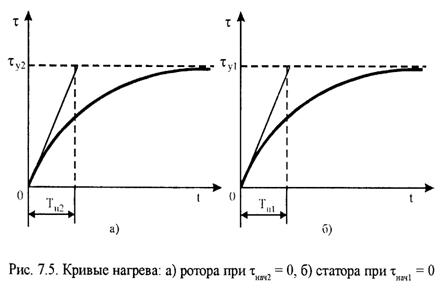
, то 
и уравнение (7.31) принимает вид (Рис.7.5а)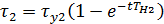 
Аналогично можно записать дифференциальное уравнение для нагрева статора
,(7.35) где 
, (7.36) 
(7.37)
- потери мощ. в статоре, С1 – теплоемкость статора, m1 – масса статора, RT1 – тепловое сопр. между внутренней и внешней поверхностями статора, - температура внутренней поверхности статора, 
- температура охлаждающей среды.
Решение (7.35) имеет вид 
, где 
, (7.39) 
, (7.40) 
, (7.41),где 
- начальное значение температуры перегрева статора, ТН1 – постоянная времени нагрева статора.
При 
получаем следующее уравнение нагрева (Рис.7.5б): 
,
Дифф. уравнениям (7.28) и (7.35), описывающим двухмассовую тепловую модель ЭД, соответствует эквивалентная тепловая схема, показанная на Рис.7.6.
Из изложенного видно, что сущность метода тепловых эквив. схем состоит в составлении тепловых схем, подобных электрическим.
Для установившегося состояния уравнение эквив. тепловой схемы имеет вид 
, (7.43)
где 
- средние температуры в точках Х и Y, 
- тепловой поток между точками Х и Y, Rxy – тепловое сопротивление между точками X и Y схемы.
Уравнения вида (7.43) составляют для всех частей ЭД. Решение полученной системы уравнений, т.е. определение установившихся температур в разных точках эквивалентной схемы, возможно, если заранее определены тепловые сопротивления.
Дата добавления: 2018-04-15; просмотров: 320; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!