Момент импульса и кинетическая энергия твердого тела
1. Момент импульса ТТ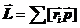 
можно связать с его моментом инерции I и угловой скоростью вращения тела w. Сравним формулы второго закона динамики вращательного движения ТТ: 
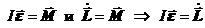(24.1)
При малых скоростях вращения, когда линейная скорость любой точки тела меньше скорости света, v << c, момент инерции тела не зависит от времени. Поэтому величину I можно ввести под знак производной: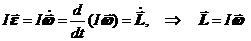 
. (24.2)
Итак: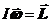 
. (24.3)
Если момент внешних сил, действующих на тело, равен нулю, то момент импульса и угловая скорость вращения тела не меняются,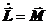 
= 0, или 
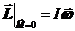= const. (24.4)
Это закон сохранения момента импульса ТТ.
Если вращается не одно тело, а система тел, момент инерции которой под действием внутренних сил может изменяться, то при изменении момента инерции системы I одновременно будет изменяться угловая скорость w так, чтобы сохранялась величина момента импульса: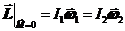 
=¼= const. (24.5)
Это закон сохранения момента импульса изолированной системы тел.
2. Кинетическая энергия ТТ может быть представлена как сумма кинетических энергий всех точек тела.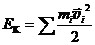 
. (24.6)
Здесь 
представляет собой скалярное произведение вектора скорости vi самого на себя, то есть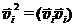 
= vi2. Т.к. скорость любой точки тела слагается из скорости движения полюса v0 (т.е. скорости поступательного движения центра СК, связанной с какой-либо точкой тела) и скорости вращательного движения относительно полюса: 
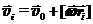, то
|
|
|
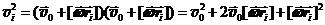. (24.7)
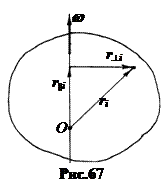
Но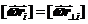 
(рис.67). Следовательно, 
.
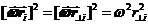Итак: 
. (24.8)
Если полюс точку О выбрать в центре масс, то средний член обратится в нуль. (Действительно, если постоянные векторы v0 и w вынести из-под знака суммы, то сумма будет представлять собой статический момент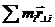 
который в этом случае обращается в нуль. Подобная ситуация была в теореме Гюйгенса-Штейнера). Выражение для кинетической энергии ТТ в этом случае упрощается.
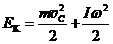. (24.9)
Кинетическая энергия ТТ равна сумме кинетической энергии поступательного движения массы тела, мысленно сосредоточенного в его центре масс и движущейся вместе с ним, и кинетической энергии тела, обусловленной его вращательным движением относительно центра масс.
Если тело движется в поле консервативных сил, то его полная механическая энергия остается постоянной, EП + ЕК = const. Например, при движении ТТ в поле силы тяжести закон сохранения механической энергии принимает вид: mgh+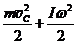 
= const. (24.10)
|
|
|
Здесь h – высота относительно нулевого уровня, vС − скорость движения центра масс.
Способы решения задач на движение осесимметричных ТТ
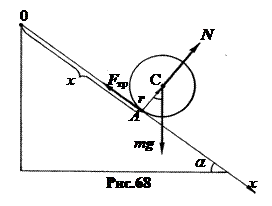В качестве примера возьмем скатывание с наклонной плоскости сплошного цилиндра массы m. Скатывание происходит без скольжения и без потерь энергии. Найдем ускорение центра масс.
1. Способ 1. Составляем уравнение моментов относительно мгновенной оси вращения A:
. (25.1)
Здесь IA – момент инерции тела относительно оси A,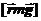 
– момент внешних сил (рис.68).
На тело действует сила тяжести mg, приложенная к центру масс тела к точке C, ее момент относительно точки A есть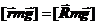 
, где R – радиус диска. Сила реакции опоры слагается из нормальной силы реакции N и касательной силы трения Fтр. Обе силы реакции приложены к точке A и их момент равен нулю. В проекции на мгновенную ось вращения получаем: 
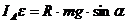. Отсюда линейное ускорение центра масс
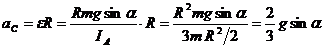. (25.2)
Тело (точка C − его центр масс) движется равноускоренно. Линейная скорость любой точки тела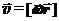 
, где r – радиус-вектор от мгновенной оси вращения А до данной точки.
|
|
|
Из системы уравнений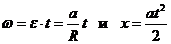 
находим 
.
Отсюда, линейная скорость любой точки тела есть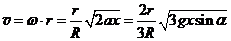 
. (25.3)
2. Способ 2. Составляем уравнение моментов относительно оси, проходящей через центр масс тела точку C,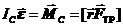 
. (25.4)
Моменты сил тяжести и нормальной реакции равны нулю (рис.69). Но сила Fтр неизвестна. Поэтому для решения задачи нужно еще одно уравнение. Воспользуемся теоремой о движении центра масс. В проекции на ось Х уравнение движения центра масс имеет вид: maC = mgsina – Fтр. (25.5)
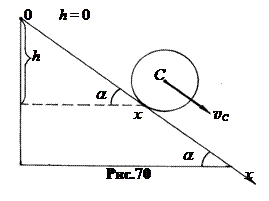Итак, получили систему из двух уравнений, которую разрешим относительно aC.
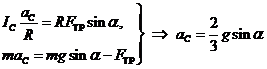. (25.6)
3. Способ 3. Если скатывание происходит без потерь механической энергии, то для решения задачи можно использовать закон сохранения механической энергии (рис.70).
Полагаем в точке х = 0 EП = 0 и EК = 0. Тогда в любой точке х полная механическая энергия равна: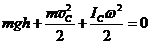 
. (25.7)
Так как h = – xsina, то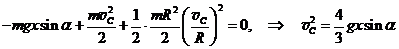 
.
Скорость пропорциональна корню квадратному из пути,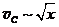 
. Но это присуще равноускоренному движению. Следовательно, 
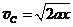. Отсюда 
. (25.8)
В том, что к процессу, в котором действуют силы трения, применяется закон сохранения механической энергии, нет противоречия. Здесь силы трения приложены к точкам тела, лежащим на мгновенной оси вращения, и потому работа сил трения равна нулю. Если же есть проскальзывание, то работа сил трения не равна нулю, и закон сохранения механической энергии не выполняется.
|
|
|
4. Итак, уравнение моментов, составленное относительно мгновенной оси вращения тела, полностью описывает движение тела. В этом случае достаточно одного уравнения.
Если уравнение моментов составляется для центра масс, не лежащего в общем случае на мгновенной оси вращения, то необходимо еще одно уравнение – теорема о движении центра масс.
Дата добавления: 2018-04-15; просмотров: 667; Мы поможем в написании вашей работы! |
Мы поможем в написании ваших работ!